Question

A $40\,kg$ box rests on the horizontal floor of a truck which is initially at rest on a horizontal road. The coefficient of kinetic friction between the floor and the box is $0.2$. The truck at time $t = 0$ accelerates constantly at $5\,m{\text{ }}{s^{ - 2}}$ and the box is $6m$ away from the rear opening of the truck. Find the time $t$ when the box just falls off the floor of the truck.

Answer 1

Hint: To solve this question, one must have a concept of motion, friction and force then one can easily solve these types of questions. Here to solve firstly we have calculated the net force and then the net acceleration and after that using Newton’s equation of motion we have found the time required for the box to fall from the truck.

Formula used:
$F = ma$
$s = ut + \dfrac{1}{2}a{t^2}$
Where, $F$ is the force,$u$ is the initial velocity, $t$ is the time, $a$ is the acceleration and $s$ is the displacement.

Complete step by step answer:

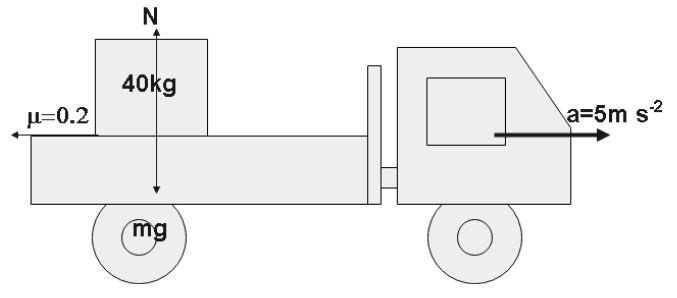
According to the question we have,
$m = 40\,kg$
$\Rightarrow \mu = 0.2$
$\Rightarrow u = 0$
$\Rightarrow s = 6\,m$
$\Rightarrow a = 5\,m{\text{ }}{s^{ - 2}}$
And we have to find the time at which the box falls down.
We Know that the net force will be,
${F_{net}} = {F_t} + {F_f}$
Whereas ${F_t}$ is the force due to the speed of the truck and ${F_f}$ is the frictional force acting on the block.And we know that,
${F_f} = \mu \times {F_N}$
Whereas ${F_N}$ is the normal. Which is equal to $mg$
${F_t} = ma$
Now substituting all the values and solving for the force,
${F_{net}} = ma + \mu \times {F_N} \\
\Rightarrow {F_{net}} = 40 \times 5 + 0.2 \times 40 \times 9.8 \\
\Rightarrow {F_{net}} = 200 - 78.4 \\
\Rightarrow {F_{net}} = 121.6N \\ $
Now we have to find the time at which the box falls down and we know that as per the question, to fall from the truck the box must travel $6m$ and then it will fall down.
And to find that will be needed net acceleration that we can find from the relation between force and acceleration.
$F = ma$
$\Rightarrow 121.6 = 40 \times a \\
\Rightarrow a = 3.04\,m{\text{ }}{s^{ - 2}} \\ $
So, to find we will simply apply Newton’s law of motion and find the time,
$s = ut + \dfrac{1}{2}a{t^2}$
Now substituting all the values in the above equation.
$6 = 0 \times t + \dfrac{1}{2} \times 3.04 \times {t^2} \\
\Rightarrow {t^2} = 3.94 \\ $
Which is approximately,
${t^2} = 4 \\
\therefore t = 2\sec \\ $
Hence the time required to fall the box from the truck is $2\sec $.

Note: The equations of motions are only valid for the constant acceleration and not use the acceleration given because as that is for trucks only as here, we have to use the net amount of acceleration and take care of formulas and proceed accordingly to get the required solution.