Question

A 4 digit number made of digits 1, 2, 3, 4, 5 is written down randomly without repetition. The probability that the number so formed is divisible by 6 is
(a) \[\dfrac{1}{20}\]
(b) \[\dfrac{1}{10}\]
(c) \[\dfrac{3}{20}\]
(d) \[\dfrac{3}{10}\]

Answer 1

Hint: We will start this question by first calculating the total possibility of 4 digit number formed used 1, 2, 3, 4, 5 then we will use the formula to determine probability which is given as –
Probability is = (Total number of favorable outcomes / Total number of outcomes).
Also, we will use the rules of divisibility of 2 and 3 and 6 as given below.
Rule of divisibility of 6: A number is divisible by 6 if it is divisible by both 2 and 3.
Rule of divisibility of 2: A number is divisible by 2 if its last digit is 0, 2, 4, 6, or 8.
Rule of divisibility of 3: A number is divisible by 3 if the sum of all digits is divisible by 3.

Complete step-by-step solution:
Let us first consider 4 digit number as in blocks given as below –

To make 4 digit number using 1, 2, 3, 4, and 5.
The total number of ways to make 4 digit number without repetition can be obtained as,
 

Here at the first position from left the total possible number of numbers possible is 5, as well as 1, 2, 3, 4, and 5, are possible.
Now at the second position from left only 4 possibilities of numbers are there as any one of them has already occurred at \[{{1}^{st}}\] place and repetition is not allowed.
Similarly, we have,

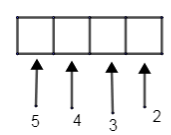
Therefore the total possibility of 4 digit number using 1, 2, 3, 4, 5 is \[5\times 4\times 3\times 2=120\].
Now finally we have to find the probability that the number so formed is divisible by 6. For this, we will use the rule of divisibility of 6.
Rule of divisibility of 6: A number is divisible by 6 if it is divisible by both 2 and 3.
So finally we will use the divisibility rule of 2 and 3.
Rule of divisibility of 2: A number is divisible by 2 if its last digit is 0, 2, 4, 6 or 8.
Rule of divisibility of 3: A number is divisible by 3 if the sum of all digits is divisible by 3.
Here we have numbers as 1, 2, 3, 4, 5.
Then the required 4 digit number is divisible by 2 if the last digit is either 2 or 4.
Consider case 1: - When the last digit is 2.
The possibility is as,

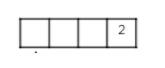
Then the only possible arrangement such that the sum of digits of 4 digit number formed is 1452. Thus sum of digits = 1 + 4 + 5 + 2 = 12 is divisible by 3. Hence 1452 and its arrangement obtained by fixing ‘2’ is the only possible number in case 1.
Consider case 2: when the last digit is 4.
Analyzing all cases where we see that no arrangement is possible in this case.
So the only possible 4 digit number formed using 1, 2, 3, 4, and 5 is 1452 and its arrangements by fixing ‘2’. Here in this case we can fix 2 at the right must end and vary all else digits.
All possible rearrangement = 3! = 3 \[\times \] 2 = 6.
This is so as ‘2’ is fixed at the rightmost end and we have 3 places for arrangements.
So the number of favorable outcomes = 6.
Probability is = (Total number of favorable outcomes / Total number of outcomes)
Here the total number of outcomes is the total possibility of 4 digit numbers using 1, 2, 3, 4, and 5 is 120.
\[\Rightarrow \] Probability = \[\dfrac{6}{120}\].
\[\Rightarrow \] Probability = \[\dfrac{1}{20}\], which is option (a).
So, the probability that the number so formed is divisible by 6 is \[\dfrac{1}{20}\], option (a).

Note: The biggest possibility of error in this question is at the point where we have to calculate the total number of 4 digit numbers formed using 1, 2, 3, 4, and 5 without repetition. Here “without repetition” is important as if any number occurred at someplace them it’s cannot repeat at any other place. So it is important to take value as \[5\times 4\times 3\times 2\] and not \[5\times 5\times 5\times 5\].