Question

A- 3RC
B- \[\dfrac{3RC}{2}\]
C- \[\dfrac{RC}{3}\]
D- RC

Answer 1

Hint: The time constant of the RC circuit is a useful quantity and determines the time taken by the capacitor to charge and discharge fully.

Complete step by step answer:
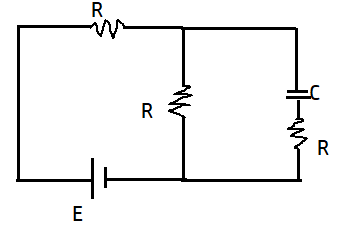
To find out the time constant which is equal to the product of capacitance and resistance present in the circuit we need to first find out the net resistance of the circuit as there are more than one resistance present in the circuit.
So in finding the net resistance we redraw our circuit by removing all the things except resistances and the battery.
The figure looks like this:
Here all the resistances are equal, so \[{{R}_{1}}={{R}_{2}}={{R}_{3}}=R\]
Now to find out the net resistance, in the figure below \[{{R}_{2}}\And {{R}_{3}}\] are in parallel,
So

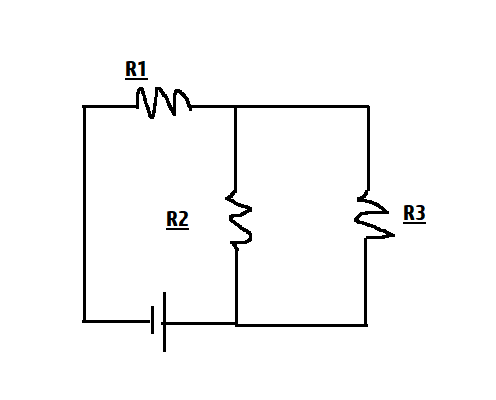
R’= \[\dfrac{{{R}_{2}}{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}}=\dfrac{R}{2}\]
Now R’ and \[{{R}_{1}}\] are in series, so net resistance= \[{{R}_{1}}\]+R’= \[\dfrac{3R}{2}\]
So total resistance of the circuit is \[\dfrac{3R}{2}\].
Now we have net resistance and since there is only one capacitor so we have capacitance.
Time constant of a RC circuit is represented by \[\tau \]
\[\tau =RC\]
\[\tau =\dfrac{3RC}{2}\]

So, the correct answer is “Option C”.

Note:
Time constant is also called transient response. In a given RC circuit, R is the value of the resistor in ohms and C is the value of the capacitor in Farads. So, the unit of Time constant is ohms-Farad represented by \[\Omega F\], and another unit is seconds. It helps us figure out how long it will take a capacitor to charge or to discharge up to a certain voltage level.