Question

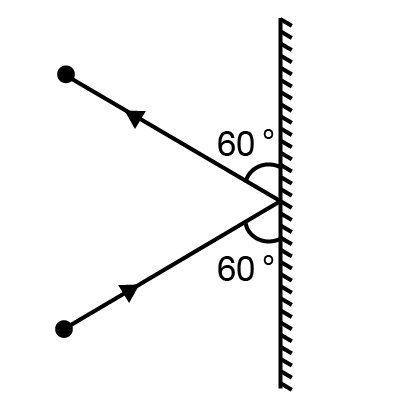
A \[3kg\] ball strikes a heavy rigid wall with a speed of \[10m/s\;\] at an angle of \[{60^ \circ }\]. It gets reflected with the same speed and angle as shown here. If the ball is in contact with the wall for \[0.20s\], what is the average force exerted on the ball by the wall?

A.\[150N\]
B.\[0\]
C.\[\;\;150\sqrt 3 N\]
D.$300N$

Answer 1

Hint: Impulse is described as the quantity of force that is acting on an object for a definite amount of time that affects a change in momentum. Now, we will first find the change in momentum when it is perpendicular to the wall and the applied force by the wall is found concerning time. Here, the direction of the force will be equal to the direction of momentum.

Complete answer:
Impulse is the change in momentum created when a large force is applied to a body for a short amount of time. In such situations, it is hard to decide force and time duration separately. Change in the momentum which is perpendicular to the wall is known by the difference of their initial and final momentum. Velocity is a vector quantity and when it rebounds back from the wall its direction changes. Thus, when we estimate the change in velocity vector, the direction must also be considered.
As momentum is a vector quantity, the impulse is also a vector.
Let us consider from the given explanation that for the mass of the ball $m = 3kg$ and velocity $v = 10m/s$ and
for an interval $t = 0.20s$
Change in momentum along the wall \[ = mv\;cos{60^ \circ } - mv\;cos{60^ \circ } = 0\]
Change in momentum perpendicular to the wall \[ = mv\;sin{60^ \circ } - \left( { - mv\;sin{{60}^ \circ }} \right) = 2mv\;sin{60^ \circ }\]
Therefore applied force or Impulse is equal to the
 $\dfrac{{Change\;\,in\;\,momentum}}{{Time}}$
\[ = \dfrac{{2mv\;sin{{60}^ \circ }}}{{0.20}}\]
\[ = \dfrac{{2 \times 3 \times 10 \times \sqrt {3} }}{{2 \times 0.20}} = 50 \times 3\sqrt 3 \]
\[ = 150\sqrt 3 N\].

Hence option C is correct.

Note:
Where impulse is taken into consideration, change in momentum is calculated. Collisions in which objects bounce back with the same speed (also equal momentum and kinetic energy) as they had earlier to the collision are called elastic collisions. In general, elastic collisions are categorized by a large velocity change, a large momentum change, a large impulse, and also a large force.