Question

A 32 kg disc moving with the velocity $v=25m/s$ toward the two stationary discs of mass 8 kg on a frictionless surface. The discs collide elastically. After the collision, the heavy disc is at rest and the two smaller discs scatter outward at the same speed. What is the x-component of the velocity of each of the 8 kg discs in the final state?

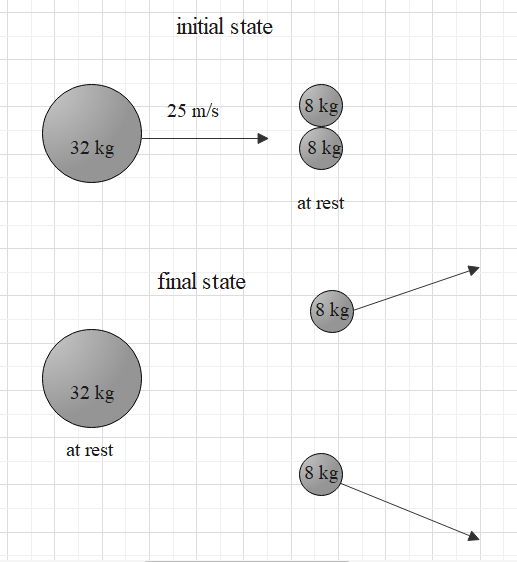
a) 12.5 m/s
b) 16 m/s
c) 25 m/s
d) 50 m/s
e) 100 m/s

Answer 1

Hint: By applying conservation of momentum formula for the initial and final conditions given: ${{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{initial}}={{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{final}}$ and find final velocity.

Complete step by step answer:
We have the following data:
$\begin{align}
  & {{m}_{1}}=32kg \\
 & {{m}_{2}}=8kg \\
 & {{m}_{3}}=8kg \\
\end{align}$
Initial condition:
$\begin{align}
  & {{v}_{1}}=25m/s \\
 & {{v}_{2}}={{v}_{3}}=0 \\
\end{align}$
Fina condition:
$\begin{align}
  & {{v}_{1}}=0 \\
 & {{v}_{2}}={{v}_{3}}=v \\
\end{align}$
So, by applying the conservation of momentum formula:
${{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{initial}}={{\left( {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \right)}_{final}}$
We get:

$ \left( 32\times 25 \right)+\left( 8\times 0 \right)+\left( 8\times 0 \right)=\left( 32\times 0 \right)+\left( 8\times v \right)+\left( 8\times v \right) \\ $
$ \implies 800+0+0=0+8v+8v \\ $
$ \implies 800=16v \\
v=50m/s
$
Therefore, the x-component of the velocity of each of the 8 kg discs in the final state is 50 m/s.

So, the correct answer is “Option D”.

Note:
The conservation of momentum states that, within some problem domain, the amount of momentum remains constant; momentum is neither created nor destroyed, but only changed through the action of forces as described by Newton's laws of motion.
An elastic collision is a collision in which there is no net loss in kinetic energy in the system as a result of the collision. Both momentum and kinetic energy are conserved quantities in elastic collisions.
Therefore, we can solve the given question by conservation of energy also.