Question

A 30^o, 60⁰ triangular set square of negligible mass is suspended freely from the right angled corner and weights are hung at the two corners as shown in figure. The ratio of masses, $\dfrac{{{m_1}}}{{{m_2}}}$ of the weights, if the hypotenuse of the set square sets horizontally, is

A. 3:1
B. 1:3
C. 1:$\sqrt 3 $
D. $\sqrt 3 $:1

Answer 1

Hint: In order to solve this problem we need to assume the tension in the sides and resolve it we will get equations and then by eliminating the terms of tension we will get the ratio of the masses. We also have to equate the horizontal components of tension since the hypotenuse is horizontal. Doing this will solve your problem.

Complete answer:

The figure for this problem including all the forces present in the system is:

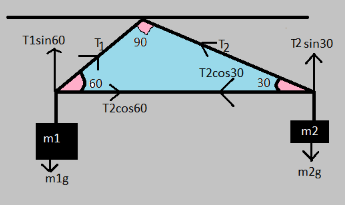
 We can see that the hypotenuse is horizontal so it means both the horizontal forces are equal.

$T_1$cos60^O = $T_2$cos30⁰

$ \dfrac{T_1}{T_2}$ = $\dfrac{cos 30^\circ}{cos 60^\circ}$ = $\dfrac{\sqrt 3 \times 2}{2 \times 1} $= $\sqrt 3 $
$ \dfrac{T_1}{T_2} $=$ \sqrt 3 $………(1)

$T_1$ sin60⁰ = ($m_1$)g …….(2)
$T_2$sin30⁰ = ($m_2$)g……..(3)

Dividing equation 1 rom equation 2 we get,
$\dfrac{{T_1\left( {\sqrt 3 } \right)\left( 2 \right)}}{{T_2\left( 2 \right)\left( 1 \right)}} = \dfrac{{m_1}}{{m_2}}$
Form 1 we have $\dfrac{{T_1}}{{T_2}} = \sqrt 3 $
So, we get
$\dfrac{{m_1}}{{m_2}} = \dfrac{{\sqrt 3 .\sqrt 3 }}{1} = \dfrac{3}{1}$
So, the correct answer is 3:1.

So, the correct answer is “Option A”.

Note:
When you get to solve this problem you need to draw the diagram and make all the forces present in it doing this will solve half of the problem and then you have to make equations according to the conditions and get the ratio of masses. The pulling force that acts along a stretched flexible connector, such as a rope or cable, is called tension, T. When a rope supports the weight of an object that is at rest, the tension in the rope is equal to the weight of the object: T = mg. Knowing this will solve your problem and will give you the right answer.