Question

A 30 m deep well is having water up to 15 m. An engine evacuates it in one hour. The power of the engine, if the diameter of the well is 4m is:
A. 11.55 kW
B. 1155 kW
C. 23.10 kW
D. 2310 kW

Answer 1

Hint: In this question, the power is to be found out. Power is defined as the rate of work done or the rate of energy spent.
The power of the engine is in electric form and since, we know that energy is converted from one form to another, we have to convert the energy in fluid form to the electric form in order to obtain a solution to this problem.

Complete step by step answer:
Consider a deep well of 30 m depth and diameter 4m with water only up to 15m.

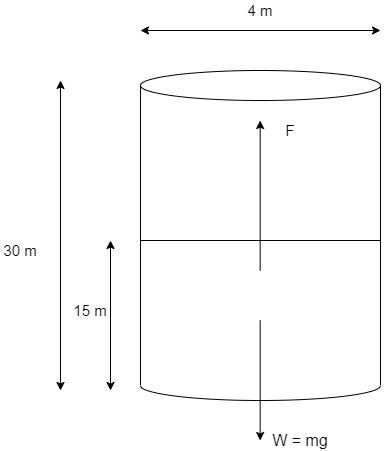
The water present in the well has weight $W = mg$ acting downwards. So, the engine that has to pump the water should counter this weight by applying the force F. The work is done on the water which will help in extracting the water out of the well. This work should be performed by the engine.
Work done, $E = F \times H$
Since the work done on the water to bring the water up is continuous, we need to consider that the distance H is the average of the total height of the well and the level of water in the well.
$\Rightarrow H = \dfrac{{30 + 15}}{2} = 22.5m$
As per the diagram, the force applied to extract water, $F = W = mg$
where acceleration due to gravity, $g = 9 \cdot 81m{s^{ - 2}}$
The mass of the water in the well, $m = V\rho$
where V is the volume of water and $\rho$ is the density of water which is equal to $1000kg{m^{ - 3}}$.
The volume of water present in the well,
$V = Ah$
where $A$ is the area of cross-section of the well and $h$ is the depth of the well.
$\Rightarrow V = \dfrac{\pi }{4}{d^2} \times h$
Diameter, $d = 4m$
$\Rightarrow V = \dfrac{\pi }{4}{4^2} \times 15 = 188 \cdot 49{m^3}$
Force applied to extract water, $F = V\rho g$
$\Rightarrow F = 188 \cdot 49 \times 1000 \times 9 \cdot 81 = 1 \cdot 849 \times {10^6}N$
The work done by the engine in applying this force to extract is $E$.
$\Rightarrow E = F \times H = 1 \cdot 849 \times {10^6} \times 22 \cdot 5 = 41602.5 \times {10^3}J$
The power required is equal to the rate of work done by the engine per unit time.
$P = \dfrac{E}{t}$
As given, the engine evacuates in one hour.
$\Rightarrow t = 1hr = 60 \times 60 = 3600\sec$
Power required, $P = \dfrac{{41602.5 \times {{10}^3}}}{{3600}} = 11.55kW$

Therefore, the power of the engine is 11.55kW. Hence, option (A) is correct.

Note:
There is an alternative way to approach this problem.
When the water is in the tank, it has potential energy. To pump the water out of it, the energy equal to potential energy must be supplied to the water per unit time.
So, the power
$P = \dfrac{E}{t}$
where E is the potential energy of water and t is the time in seconds.
Potential energy, $E = mgh$
Mass, $m = V \times \rho$
$V = \dfrac{\pi }{4}{d^2} \times h$
Diameter, $d = 4m$
$\Rightarrow V = \dfrac{\pi }{4}{4^2} \times 15 = 188 \cdot 49{m^3}$
Mass, $m = 188 \cdot 49 \times 1000 = 188490kg$
Height, $h = \dfrac{{30 + 15}}{2} = 22 \cdot 5m$
Acceleration due to gravity, $g = 9 \cdot 81m{s^{ - 2}}$
Substituting all in the equation, we get –
$\Rightarrow P = \dfrac{{mgh}}{t} = \dfrac{{188490 \times 9 \cdot 81 \times 22 \cdot 5}}{{3600}} = \dfrac{{4160445}}{{3600}} = 11556 \cdot 79W = 11 \cdot 55kW$