Question

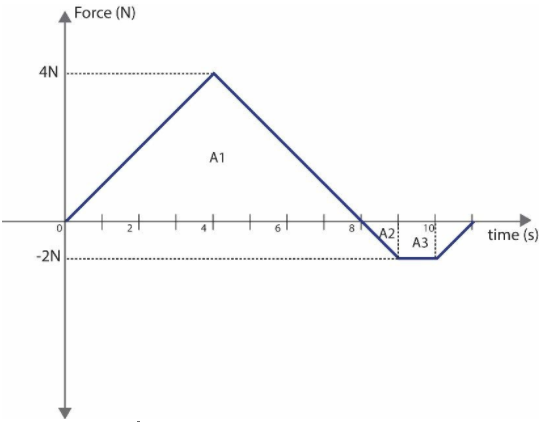
A 2kg toy car moves along x-axis. Graph shows resultant force , acting on the car which begins at rest at time t=0. The velocity of the car at t=10s is:

A. $1m{{s}^{-1}}$
B. $-1.5m{{s}^{-1}}$
C. $6.5m{{s}^{-1}}$
D. $13m{{s}^{-1}}$

Answer 1

Hint: This entire problem is based on Newton’s second law of motion only twist is the force here is varying with time. The variation of force is linear and so is the acceleration. Find the velocity of the object by calculating the area under the acceleration time curve.

Complete step-by-step answer:

The given graph describes how the force on a car is varying with time.

Now from Newton’s second law of motion, $F\left( t \right)=m\dfrac{dv}{dt}$. Where $\dfrac{dv}{dt}=a(t)$, that is it is equal to the instantaneous acceleration at a given time t.
Therefore, the relation between the force and acceleration becomes:
$\begin{align}
  & \text{Acceleration}=\dfrac{\text{Force}}{\text{Mass}} \\
 & a=\dfrac{F}{m}=\dfrac{F}{2} \\
\end{align}$
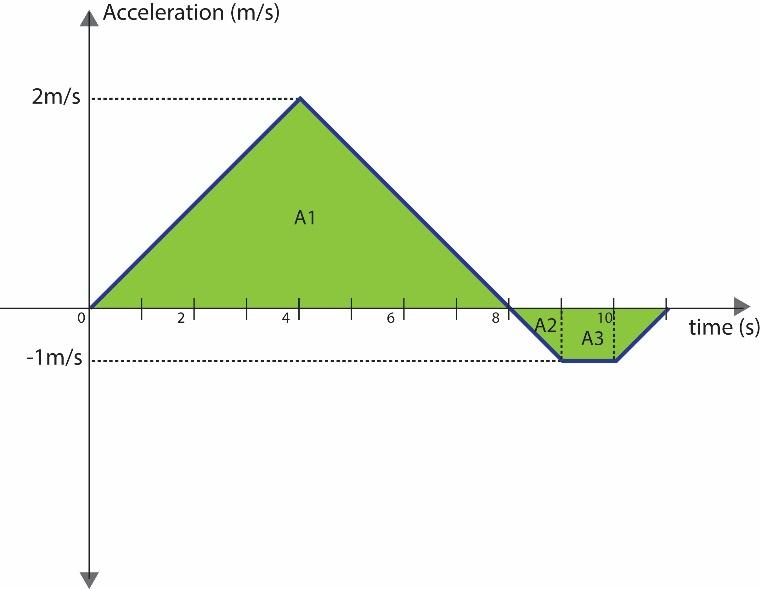
Thus, the force time graph can be converted into the acceleration time graph, and it becomes:

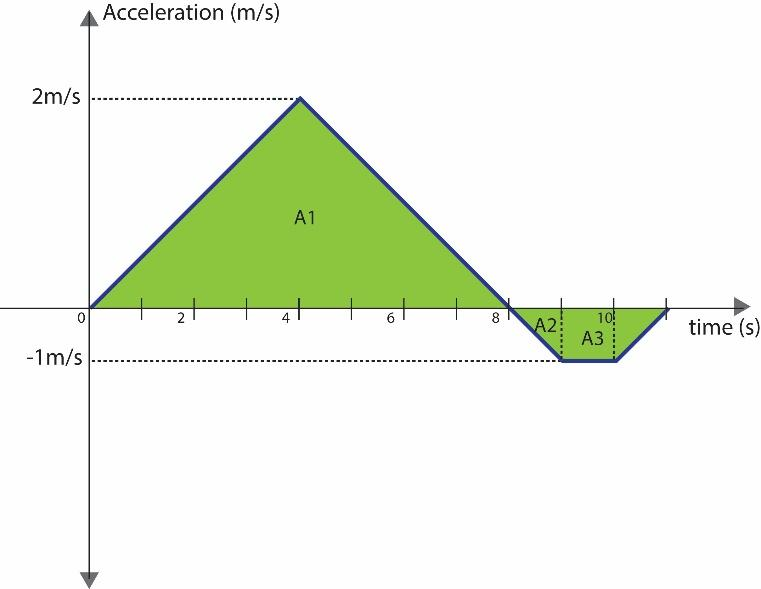
Observe that for the entire duration the acceleration is linear since the force is also linear.
From the following relation, we can derive the expression of velocity at an instant as a function of acceleration and time.
$\begin{align}
  & \dfrac{dv}{dt}=a(t) \\
 & v(t)=\int{adt} \\
\end{align}$
It can be inferred that the velocity at a point in time is the area under the acceleration time graph till that time instant.
We are asked to find the velocity at $t=10\sec $
Let us divide the total area to be calculated in parts.

Part1: $t=0\sec \text{ to }t=8\sec $
It is a triangle with the height $2m/{{s}^{2}}$ and the base $8\sec $ . Therefore, the area of the triangle for this part becomes:
$\begin{align}
  & \text{Area}=\dfrac{1}{2}\text{base}\times \text{height} \\
 & {{A}_{1}}=\dfrac{1}{2}\times 8\times 2=8m/s \\
\end{align}$

Part2: $t=8\sec \text{ to }t=9\sec $
It is a triangle with the height $-1m/{{s}^{2}}$ and the base $1\sec $ . Therefore, the area of the triangle for this part becomes:
$\begin{align}
  & \text{Area}=\dfrac{1}{2}\text{base}\times \text{height} \\
 & {{A}_{2}}=\dfrac{1}{2}\times -1\times 1=-\dfrac{1}{2}m/s \\
\end{align}$

Part3: $t=9\sec \text{ to }t=10\sec $
It is a rectangle with the height $-1m/{{s}^{2}}$ and the length $1\sec $ . Therefore, the area of the rectangle for this part becomes:
$\begin{align}
  & \text{Area}=\text{length}\times \text{height} \\
 & {{A}_{3}}=1\times 1=-1m/s \\
\end{align}$
Therefore, the sum of the areas for all the parts gives us the velocity at time 10 sec.
That is:
$\begin{align}
  & v={{A}_{1}}+{{A}_{2}}+{{A}_{3}} \\
 & v=8-\dfrac{1}{2}-1=6.5m/s \\
\end{align}$

Therefore, the correct answer to this question is option C. 6.5m/s.

Note: When force is decreasing from four seconds to eight second, the velocity of the car is still increasing but at a lower rate as compared to that of zero to four seconds. Only after $t > 8 sec$ the direction of the acceleration reverses i.e. it becomes negative and the velocity starts reducing. Try to avoid integration for finding the area of the triangles, this can save a lot of time.
Students make the mistake thinking that velocity is zero when force is zero, this is not true.