Question

A 2cm diameter coin rests flat on the bottom of a bowl in which the water is \[20cm\] deep. $\left( {{u_{\text{w}}} = \dfrac{4}{3}} \right)$. If the coin is viewed directly from the above, what is the apparent diameter?
$(A)2cm$
$(B)1.5cm$
$(C)2.67cm$
$(D)1.67cm$

Answer 1

Hint: When a ray travels one medium to another medium obliquely, refraction occurs i.e. the ray changes its path from the initial. When a ray of light incidents on a plane surface along the normal, from one medium to another, no refraction takes place and it passes through both the medium un-deviated. To solve the problem, the relationship between the apparent height along the vertical direction, the depth, and the refractive index of the medium has to be used.
Formula used:
The formula used to find the apparent vertical depth \[\left( h \right)\] of a body put in a medium of depth $\left( d \right)$ and refractive index $\left( \mu \right)$ is given as:
$h = d\left( {1 - \dfrac{1}{\mu }} \right)$

Complete step-by-step solution:
The initial diameter of the coin, ${d_1} = 2\;{\text{cm}}$
Depth of the water bowl, \[d = 20{\text{ }}cm\]
Let the final diameter of the coin when viewed from above be ${d_2}$

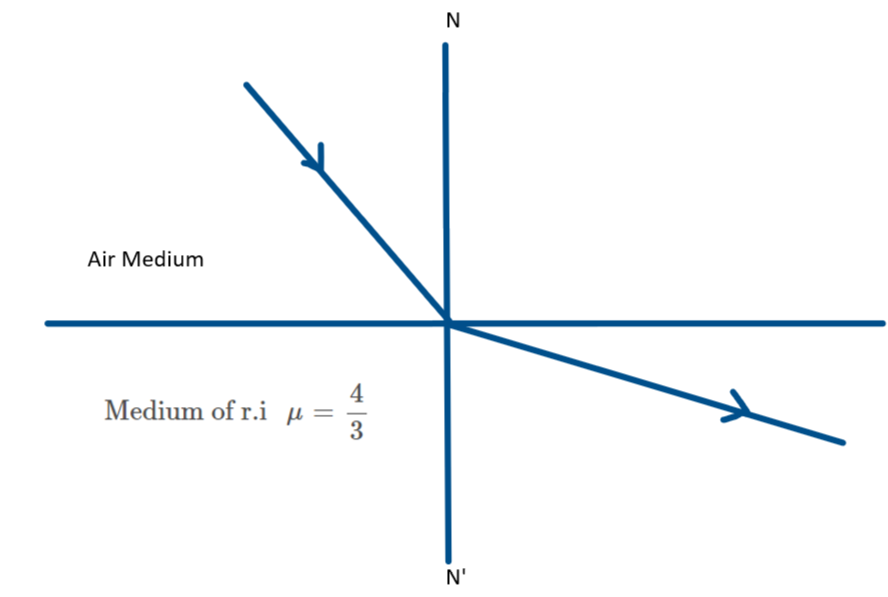
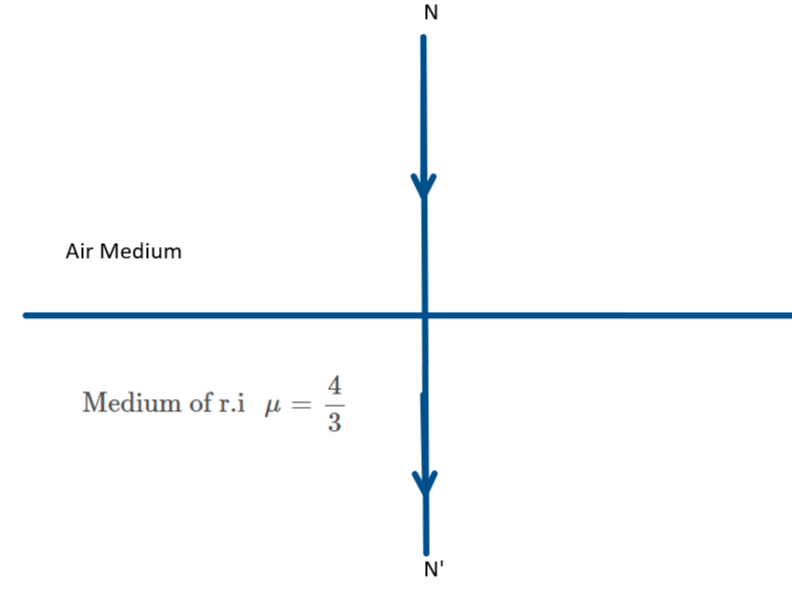
Now, let us consider the following two diagrams given below:
 In the first diagram, the incident ray hits the plane surface at an angle to the normal NN’ (in medium one- air) and then refracts away from/ or towards the normal, based on the refractive index of the second medium. However in the second case, the incident ray is along the normal NN’ and upon refraction at the boundary, goes through un-deviated.
So, when the coin is viewed directly from above the bowl, there is only a change in the apparent vertical depth of the coin (i.e., the new height at which the coin is now visible) but there is no change in the horizontal depth (i.e., the diameter of the coin).
The new diameter of the coin, when viewed from directly above the bowl, is equal to \[2cm\], i.e., ${d_2} = 2\;{\text{cm}}$
Hence the correct answer is option (A).

Note:
> The refractive index of a medium is the ratio of the speed of light in a vacuum to the speed of light in that medium. It is always greater than one (except if the medium itself is a vacuum).
> When the ray goes rarer to denser medium it refracts away from the normal. And, when it goes denser from a rarer medium its refracts towards the normal.