Question

A 2 unit high marble slab with $\text{1 unit}\times \text{4 unit}$ base is fixed to the floor of a courtyard. The surface area of the marble which is visible is:
(a) 28 sq. units
(b) 26 sq. units
(c) 24 sq. units
(d) 20 sq. units

Answer 1

Hint: In the problem above, let us assume that height of the marble is “h” which is given in the question as 2 units. Then base dimensions are given as $\text{1 unit}\times \text{4 unit}$ which is equal to $length\times breadth$ so let us assume length of the slab is “l” and breadth of the slab is “b”. Now, to find the visible area first of all find the total surface area of the elevated marble; the elevated marble is in the form of the cuboid. We know that the total surface area of the cuboid is given as $2\left( lb+bh+hl \right)$ and then subtract the result of this total surface area with the area of the base. The result of subtraction is the required answer.

Complete step-by-step answer:
In the above problem, the height of the marble slab is given as 2 units, the length and breadth of the marble slab is given in the form of $\text{1 unit}\times \text{4 unit}$. In this form, length is equal to 1 unit and breadth is equal to 4 units. Now, let us assume the length, breadth and height of the marble slab are “l, b and h” respectively.
In the below diagram, we are showing a marble slab having l, b and h as the length, breadth and height respectively.

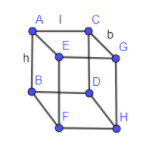
In the above diagram, we have shown AC as the length of the cuboid, AB as the height of the cuboid and CG as the breadth of the cuboid.
We know that total surface area (T.S.A) of the cuboid is equal to:
$T.S.A=2\left( lb+bh+hl \right)$
Substituting the value of length as 1 unit, breadth as 4 units and height as 2 units in the above equation we get,
$\begin{align}
  & T.S.A=2\left( 1\left( 4 \right)+4\left( 2 \right)+2\left( 1 \right) \right) \\
 & \Rightarrow T.S.A=2\left( 4+8+2 \right) \\
 & \Rightarrow T.S.A=2\left( 14 \right) \\
 & \Rightarrow T.S.A=28\text{ sq}\text{.units} \\
\end{align}$
In the above total surface area we have also counted the base of the marble which is not visible and as we have to find the visible surface area of the marble so we are going to subtract the area of the base from the total surface area of the marble.
Area of the base $=1\times 4=4\text{ sq}\text{.units}$
Subtracting the above area of base from the total surface area of the marble we get,
$\begin{align}
  & \left( 28-4 \right)\text{sq}\text{.units} \\
 & =24\text{ sq}\text{.units} \\
\end{align}$
Hence, the visible surface area of the marble is equal to 28 sq. units.
And hence, the correct option is (c).

Note: The plausible mistake in solving the above problem is to forget to subtract the surface area of the base of the marble from the total surface area. This mistake is often seen in the exams because in the rush of completing the exam on time students tend to forget to subtract the area of base.
The other way of solving the above problem is by finding the area of the surfaces of marble which is visible.

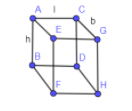
As from the figure, you can see that the surface BDHF is not visible so apart from this surface add the surface area of all the faces.
Area of (ACGE + CGHD + EGHF + AEFB +ACDB)
The above summation of areas is equal to:
$lb+2\left( bh+hl \right)$
Substituting the value of length as 1 unit, breadth as 4 units and height as 2 units in the above equation we get,
$\begin{align}
  & 1\left( 4 \right)+2\left( 4\left( 2 \right)+2\left( 1 \right) \right) \\
 & =4+2\left( 8+2 \right) \\
 & =4+2\left( 10 \right) \\
 & =4+20 \\
 & =24\text{sq}\text{.units} \\
\end{align}$