Question

A $ 1kg $ stone at the end of $ 1m $ long string is whirled in a vertical circle at a constant speed of $ 4m{s^{ - 1}} $ . The tension in the string is $ 6N $ , when the stone is
(A) At the top of the circle
(B) At the bottom of the circle
(C) Half way down
(D) None of above

Answer 1

Hint :In the given question we need to be aware of the term circular motion and the terms related to it which are the movement of an object along the circumference of a circle or rotation along a circular path. Now by using the formula of the $ T < \dfrac{{m{v^2}}}{R} $ we get the $ \theta = - {180^o} $ . which is the ultimate answer to the question.

Complete Step By Step Answer:
Firstly we should be aware of the term and the terminology of circular motion.
In the field of physics, the circular motion is considered as the movement of an object along the circumference of a circle or rotation along a circular path. It can be either uniform, with the constant angular rate of rotation and constant speed. Or as the non-uniform with a changing rate of rotation. The rotation which is around the fixed axis of a three-dimensional body involves circular motion of its parts and therefore the equations of motion describe the movement of the center of mass of a body.

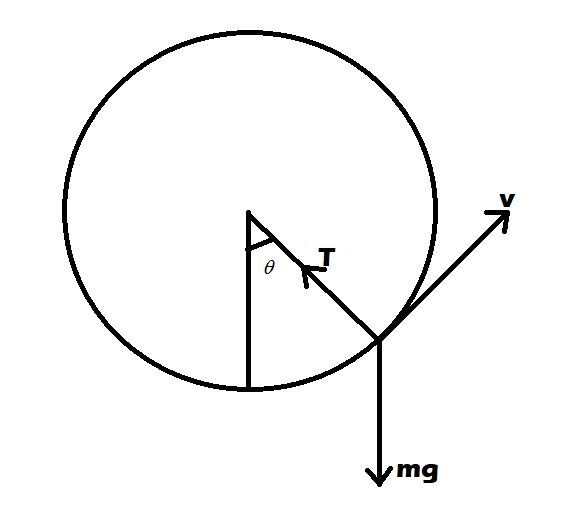
Now, first thing is to write the equation balancing the forces:
 $ \dfrac{{m{v^2}}}{R} = \dfrac{{1*{4^2}}}{1} = 16N $
By the observation we get that:
 $ T < \dfrac{{m{v^2}}}{R} $
Now at the highest point we will get:
 $
  T = mg\cos \theta + \dfrac{{m{v^2}}}{R} \\
  6 = 10\cos \theta + 16 \\
  \theta = - {180^o} \\
  $

Note :
In the case of rotation around a fixed axis of a rigid body that is not negligibly small compared to the radius of the path, each particle of the body describes a uniform circular motion with the same angular velocity, but with velocity and acceleration varying with the position with respect to the axis.