Question

A $1kg$ mass is rotated along a horizontal circle by a tightened string which has a tension$T = 16{\pi ^2}N$. Find the frequency of rotation.

Answer 1

Hint: For rotational motion, there is always a centripetal force acting along the radius inwards. Here, the mass is rotated horizontally; hence you can safely discard the effect of gravity on it. The centripetal force for this motion is actually the tension of the tightened string.

Formulae Used:
You can calculate the centripetal force from the expression:
${F_C} = mr{\omega ^2}$................................(1)
where ${F_C}$ is the centripetal force of the rotational motion, $m$ is the mass of the body under rotation $r$ is the radius of the circular path, and is the angular frequency of the rotation.
You can define the angular frequency of as
$\omega = 2\pi \nu $
where, $\nu $ is the frequency of the rotation.

Step by step answer:
Given:
The mass of the body under rotation is $m = 1kg$
The tension of the tightened string $T = 16{\pi ^2}N$
To calculate: Frequency of rotation $\nu $.
Step 1:

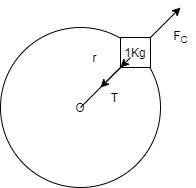
Let the length of the tightened string is $rcm$. Now you can see from the figure, this $r$ is basically the radius of the circular path traversed by the body.
Then calculate the centripetal force of the motion from eq (1).
 $
  {F_C} = mr{\omega ^2} \\
   = 1 \times r \times {\omega ^2}N \\
   = r{\omega ^2}N \\
 $
where, the body experiences an angular frequency of $\omega {s^{ - 1}}$.
Step 2:
Now the tension of the string is the required centripetal force to keep the rotational motion uniform.
Hence, you can write the expression
${F_C} = T$
Now putting the values, you can write
$
   \Rightarrow r{\omega ^2} = 16{\pi ^2} \\
   \Rightarrow {\omega ^2} = \dfrac{{16{\pi ^2}}}{r} \\
   \Rightarrow \omega = \sqrt {\dfrac{{16{\pi ^2}}}{r}} \\
  \therefore \omega = \dfrac{{4\pi }}{{\sqrt r }} \\
 $
Step 3:
You can rewrite the expression in eq (2) to get the value of the frequency of the rotation.
$\nu = \dfrac{\omega }{{2\pi }}$ (4)
Step 4:
Now put the value of $\omega $ in eq (4)
$
  \nu = \dfrac{{4\pi }}{{\sqrt r 2\pi }}{s^{ - 1}} \\
  \therefore \nu = \dfrac{2}{{\sqrt r }}{s^{ - 1}} \\
 $

Final answer: A $1kg$ mass is rotated along a horizontal circle by the tightened string, which has a tension $T = 16{\pi ^2}N$, where the string length is $rcm$ then the frequency of the rotation is $\dfrac{2}{{\sqrt r }}{s^{ - 1}}$.

Note: Generally, some of you may miss the point of horizontal rotation, then the case will be much more complicated and the gravity will be in play to accelerate the motion. There is another subtle concept that many of you may miss, that is the centripetal force acts inwards along the radial direction and here, the tension acts inwards to pull the string, which plays the role of the centripetal force to carry on the rotational motion. Many of you may think that there should be an outward force to balance the tension of the string and that is the centripetal force, but then you are wrong. The force outwards is not a centripetal force but a centrifugal reaction.