Question

A 15m long ladder reaches a window 12m high from the ground on placing it against a well. How far is the ladder from the well?

Answer 1

Hint: The distance of the ladder from the well can be found using the Pythagoras theorem. We will first draw the diagram based on the given information. We will substitute the length of ladder and height from the ground in the formula of Pythagoras theorem and find the distance.

Formula used:
We will use the formula of Pythagoras Theorem: \[{\rm{Hypotenus}}{{\rm{e}}^{\rm{2}}} = {\rm{Opposit}}{{\rm{e}}^{\rm{2}}} + {\rm{Adjacen}}{{\rm{t}}^{\rm{2}}}\]

Complete step-by-step answer:
We will first draw the diagram based on the information.

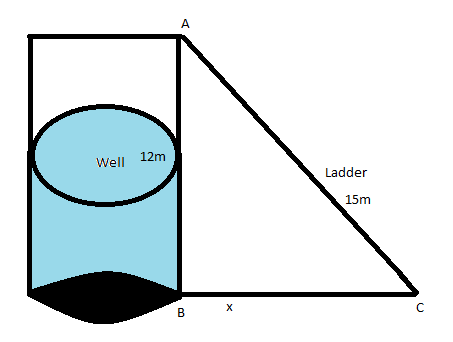
Let \[x\] denote the distance between the ladder and the wall.
We are given that the ladder is of length \[15m\] and the window is at a height of \[12m\] from the ground.
From the diagram we have A be the position of the window, B be the ground and C be the position of the ladder placed at the ground.
Let AB denote the height of the window from the ground, BC denote the distance of the ladder from the well and AC denote the length of the ladder.
So, we have \[AB = 12m\], \[AC = 15m\] and \[BC = x\].
We can see that a right angle is formed at B.
Therefore applying Pythagoras theorem in the triangle ABC, we get
\[A{C^2} = A{B^2} + B{C^2}\]
Now substituting \[AB = 12m\], \[AC = 15m\] and \[BC = x\] in the above equation, we get
 \[ \Rightarrow {15^2} = {12^2} + {x^2}\]
Rewriting the above equation, we get
\[ \Rightarrow {x^2} = {15^2} - {12^2}\]
Squaring the terms, we get
\[ \Rightarrow {x^2} = 225 - 144\]
Subtracting the terms, we get
\[ \Rightarrow {x^2} = 81\]
Taking square root on both the sides, we get
\[ \Rightarrow x = \sqrt {81} \]
\[ \Rightarrow x = 9m\]
Therefore, the distance of the ladder from the well is 9m.
Note: We are using the concept of Pythagoras theorem. Pythagora's theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides''. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle\[90^\circ \].