Question

A 14.5kg mass, fastened to the end of a steel wire of unstretched length 1.0m, is whirled in a vertical circle with an angular velocity of $2\ rev.{{s}^{-1}}$at the bottom of the circle. The cross sectional area of the wire is \[0.065c{{m}^{2}}\]. Calculate the elongation of the wire when the mass is at the lowest point of its path.

Answer 1

Hint: This problem needs knowledge of circular motion. The centrifugal force is given by $M{{\omega }^{2}}r$. The net force acting on the whole system of the steel wire and the mass fastened to it by, ${{F}_{net}}=Mg+M{{\omega }^{2}}r$. Additionally you must also know, how to use the Young’s modulus formula given by: $Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}\Rightarrow Y=\dfrac{F.l}{A.\Delta l}$. This will help us in finding the elongated length \[(\Delta l)\] due to the net force.

Step by step solution:
Let’s start by making a diagram of the problem.

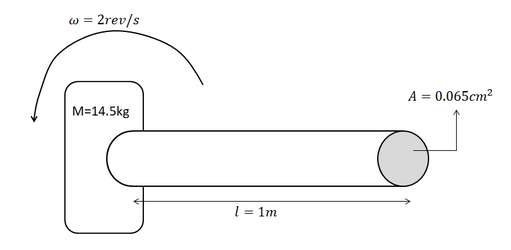
A body of mass 14.5kg (M=14.5kg) is fastened on to the steel wire of length 1m (l=1m). This whole system is whirled in a circular motion. Hence, the circular motion will have the radius as that of the wire when being whirled around. That is, l=r=1m.
The initial cross sectional area of the wire is given as: A=\[0.065c{{m}^{2}}\], that is \[A=0.065\times {{10}^{-4}}{{m}^{2}}\].
We are asked to find the elongation of the wire when the mass (M=14.5kg) is at the lowest point in the path. As per the circular motion followed by the system of the mass and the wire, the lowest point of this motion would be at the point where, the downward force due to the gravitational force would be maximum.
As per the circular motion, the angular frequency of the current circular motion is: \[\omega =2\ rev.{{s}^{-1}}\]. Hence, 2 revolutions are made in 1 second. Therefore, the value of the angular frequency in terms of radians per second is given by: \[\omega =2\ rev.{{s}^{-1}}\Rightarrow \omega =\dfrac{2(2\pi r)}{1}\Rightarrow \omega =4\pi \ rad.{{s}^{-1}}\].
Hence, the net force acting on the mass (M=14.5kg) would be the sum of the downward gravitational force and centrifugal force acting on the mass. Therefore, the net force is: ${{F}_{net}}=Mg+M{{\omega }^{2}}r$.
Substituting in the values of the mass M=14.5kg, the angular frequency \[\omega =4\pi \ rad.{{s}^{-1}}\]and the radius of the motion being r=l=1m.
Therefore, ${{F}_{net}}=Mg+M{{\omega }^{2}}r\Rightarrow {{F}_{net}}=(14.5)g+(14.5){{(4\pi )}^{2}}(1)$. Putting in the value of acceleration due to gravity $g=9.8\ m.{{s}^{-2}}$, we get: ${{F}_{net}}=142.1+2289.75\Rightarrow {{F}_{net}}=2431.85N$.
Due to this force acting on the wire, the force will cause the wire to get elongated by a length $\Delta l$. This elongated length can be found using the Young’s modulus (Y) formula. This formula is given by: $Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}\Rightarrow Y=\dfrac{F.l}{A.\Delta l}$. The standard value of Young’s modulus for steel wire is $Y=2\times {{10}^{11}}\ N{{m}^{-2}}$.
$\therefore \Delta l=\dfrac{2431.85(1)}{(0.065\times {{10}^{-4}}).(2\times {{10}^{11}})}\Rightarrow \Delta l=1.87\times {{10}^{-3}}m$.
Hence, the elongation of the wire is $1.87\times {{10}^{-3}}m$.

Note: The Young’s modulus of any material is given by the ratio of the longitudinal stress applied on the material to the longitudinal strain. The formula is: $Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}}\Rightarrow Y=\dfrac{F.l}{A.\Delta l}$, which is a specific form of the Hooke’s law of elasticity. This formula can be used, whenever the force is applied longitudinally.