Question

A 1.3 m tall girl spots a balloon moving with the wind in a horizontal line at a constant height of 91.3 m from the ground. The angle of elevation of the balloon from the eyes of the girl at an instant has measure $60{}^\circ $. After some time, the angle of elevation is reduced in measure to $30{}^\circ $. Find the distance travelled by the balloon during the interval.

Answer 1

Hint: We will make a rough diagram to understand the position of the balloon and the angle of elevation from the eyes of the girl. Then we will use trigonometric functions and their definitions to obtain relations between sides of triangles. Using these relations and the values of trigonometric functions for standard angles, we will find the distance travelled by the balloon in the interval.

Complete answer:
Let us look at a rough diagram that represents the balloon, the observer and the angles of elevation. The figure looks like the following,
   

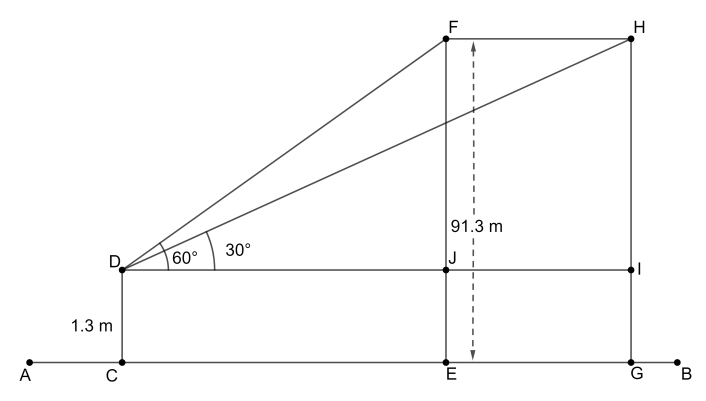
According to the figure and the given information we have the segment CD as the girl, so $\text{CD}=1.3\text{ m}$. Point F is the initial place where the balloon was seen by the girl. So, we have $\text{EF}=91.3\text{ m}$ and the angle of elevation as $\angle \text{FDI}=60{}^\circ $. Then the balloon travels to point H and the angle of elevation is $\angle \text{HDI}=30{}^\circ $. Also, we have $\text{EF}=\text{GH}=91.3$. We have to find the length of segment FH which is also the same as segment JI.
We know that $\tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}}$. Now, let us consider $\Delta \text{FDJ}$. In this triangle, we have
$\tan 60{}^\circ =\dfrac{\text{FJ}}{\text{DJ}}$
From the figure, we can see that $\text{FJ}=\text{EF}-\text{EJ}$ and $\text{EJ}=\text{CD}=1.3$. Also, $\tan 60{}^\circ =\sqrt{3}$ and $\text{EF}=91.3$. Substituting these values in the above expression, we get
$\begin{align}
  & \sqrt{3}=\dfrac{91.3-1.3}{\text{DJ}} \\
 & \therefore \text{DJ}=\dfrac{90}{\sqrt{3}} \\
\end{align}$
Next, let us consider the triangle $\Delta \text{HDI}$. In this triangle, we have
$\tan 30{}^\circ =\dfrac{\text{HI}}{\text{DI}}$
We know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$. From the figure, we can see that $\text{HI}=\text{FJ}$ and $\text{DI}=\text{DJ}+\text{JI}$. Substituting $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$, $\text{HI}=90$ and $\text{DJ}=\dfrac{90}{\sqrt{3}}$ in the above expression, we get
$\dfrac{1}{\sqrt{3}}=\dfrac{90}{\left( \dfrac{90}{\sqrt{3}}+\text{JI} \right)}$
From the figure, we can see that we have to find the length of segment FH which is also the same as segment JI. Rearranging and solving the above equation, we get
$\begin{align}
  & \dfrac{90}{\sqrt{3}}+\text{JI}=90\sqrt{3} \\
 & \Rightarrow \text{JI}=90\sqrt{3}-\dfrac{90}{\sqrt{3}} \\
 & \Rightarrow \text{JI}=\dfrac{90\sqrt{3}\times \sqrt{3}-90}{\sqrt{3}} \\
 & \Rightarrow \text{JI}=\dfrac{270-90}{\sqrt{3}} \\
 & \therefore \text{JI}=\dfrac{180}{\sqrt{3}}\text{ m} \\
\end{align}$
Hence, the distance travelled by the balloon in the interval is $\dfrac{180}{\sqrt{3}}\text{ m}$ .

Note:
It is useful to be familiar with the trigonometric ratios of standard angles for such types of questions. It is essential that we draw a rough figure. The diagram helps us to determine the sides between which we want a ratio and therefore, helps us choose a trigonometric function accordingly. Similar to the angle of elevation, there is a concept of the angle of depression as well.