Question

A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is $60^\circ $ . After some time, the angle of elevation reduces to $30^\circ $ . Find the distance travelled by the balloon during the interval.

Answer 1

Hint:
We can draw a diagram. The height of the balloon from the eye level can be found out by subtracting the height of the girl from the height from the ground to the balloon. Then we can obtain 2 right angles triangles with the initial and final position of the balloons. Then we can obtain 2 trigonometric ratios relating the base and height. Then we can solve them to find the required distance.

Complete step by step solution:
We can draw a diagram with the given details.

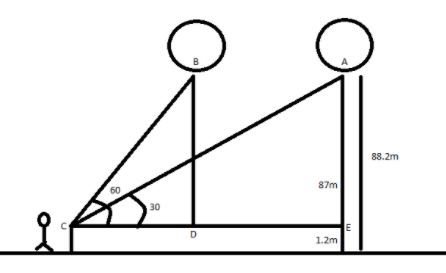
Here, B is the initial position and A is the final position of the balloon. We need to find the distance AB or DE. CE is the eye level of the girl. It is given that the height of the balloon from ground is 88.2m and height of the girl is 1.2m.
So, the height of the balloon from the eye level is given by subtracting the height of the girl from the height from the ground to the balloon
 $ \Rightarrow AE = 88.2 - 1.2$
 $ \Rightarrow AE = 87m$
As, AE=BD, hence BD=87m .
From the figure, $\angle BCD = 60^\circ $ and $\angle ACE = 30^\circ $
Now consider the right-angled triangle BCD.
  $\tan \angle BCD = \dfrac{{BD}}{{CD}}$
On substituting the values, we get,
  $ \Rightarrow \tan 60^\circ = \dfrac{{87}}{{CD}}$
We know that $\tan 60^\circ = \sqrt 3 $
  $ \Rightarrow \sqrt 3 = \dfrac{{87}}{{CD}}$
On rearranging, we get,
  $ \Rightarrow CD = \dfrac{{87}}{{\sqrt 3 }}$ … (1)
Now consider the right-angled triangle ACE
  $\tan \angle ACE = \dfrac{{AE}}{{CE}}$
On substituting the values, we get,
 $ \Rightarrow \tan 30^\circ = \dfrac{{87}}{{CE}}$
We know that $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$
 $ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{87}}{{CE}}$
On rearranging, we get,
 $ \Rightarrow CE = 87\sqrt 3 $
From the figure, we can say that, CE=CD+DE
 $ \Rightarrow CD + DE = 87\sqrt 3 $
On rearranging, we get,
 \[ \Rightarrow DE = 87\sqrt 3 - CD\]
Now we can substitute the value of equation (1).
 \[ \Rightarrow DE = 87\sqrt 3 - \dfrac{{87}}{{\sqrt 3 }}\]
On taking 87 common we get,
 \[ \Rightarrow DE = 87\left( {\sqrt 3 - \dfrac{1}{{\sqrt 3 }}} \right)\]
On taking LCM we get,
  \[ \Rightarrow DE = 87\left( {\dfrac{{3 - 1}}{{\sqrt 3 }}} \right)\]
On simplification we get,
  \[ \Rightarrow DE = 87\left( {\dfrac{2}{{\sqrt 3 }}} \right)\]
On opening the bracket we get,
 \[ \Rightarrow DE = \dfrac{{174}}{{\sqrt 3 }}\]
On simplification we get,
 \[ \Rightarrow DE = 58\sqrt 3 m\]

Therefore, the distance travelled by the balloon in the time interval is \[58\sqrt 3 m\].

Note:
The concept used here is trigonometry. We must draw the figure for better understanding of the question. We must take care that the height of the observer is given and the height of the balloon from the ground is given. We must take the height from the eye level only while substituting in the ratio. The angles of elevation are also the angles from the eye level. We must mark the angles correctly knowing that as distance increases, the angle decreases.