
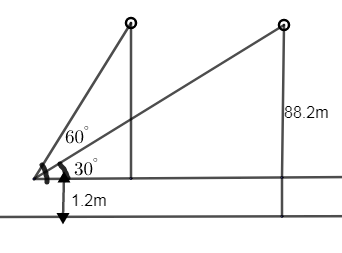
A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is \[{{60}^{\circ }}\]. After some time, the angle of elevation reduces to \[{{30}^{\circ }}\] (see figure). Find the distance travelled by the balloon during the interval.

Answer
617.4k+ views
Hint: Consider the 2 right triangles formed. Given the height and elevation, find the base of the triangle. Then calculate the distance travelled by the balloon from the \[{{1}^{st}}\]point to \[{{2}^{nd}}\]point.
Complete step-by-step answer:
It is given that the height of the girl who sees the balloon is 1.2m. So let us mark the height of the girl from ground G, as AG = 1.2m.
From the figure, AG is parallel to BF i.e. AG || BF.
Hence, AG = BF = 1.2m.
We need to find the distance travelled by the balloon i.e. we need to find the distance BC.
Given that the balloon is at a height of 88.2m from the ground.
\[\therefore EF=88.2\]m
First the girl sees the balloon at an angle of \[{{60}^{\circ }}\]. So from the figure we can say that,
\[\angle EAB={{60}^{\circ }}\]
After the balloon travels to an unknown distance, the girl sees the balloon at an elevation of \[{{30}^{\circ }}\].
\[\therefore \angle DAC={{30}^{\circ }}\]
And the distance travelled by the balloon = BC.
From the figure, we can say that, EF = BE + BF.
\[\begin{align}
& \therefore BE=EF-BF \\
& BE=88.2-1.2=87m \\
\end{align}\]
Hence, BE = DC = 87 m.
From the figure we can say that \[\angle ABE\] and \[\angle ACD\]are right angled.
\[\therefore \angle ABE={{90}^{\circ }}\] and \[\angle ACD={{90}^{\circ }}\].
Let us first consider, \[\vartriangle EAB\], from where we need to find distance AB.
We know, \[\angle EAB={{60}^{\circ }}\]and length of BE = 87m.
\[\tan A\]= Opposite side to angle A / Side adjacent to angle A = \[\dfrac{BE}{AB}\].
\[\tan 60=\dfrac{87}{AB}\Rightarrow AB=\dfrac{87}{\tan {{60}^{\circ }}}\]
From the trigonometric table, we know that \[\tan {{60}^{\circ }}=\sqrt{3}\].
\[\therefore AB=\dfrac{87}{\sqrt{3}}\]m.
Now let us consider, \[\vartriangle DAC\], where DC = 87m and \[\angle DAC={{30}^{\circ }}\].
\[\begin{align}
& \tan 30=\dfrac{DC}{AC} \\
& \Rightarrow \tan 30=\dfrac{87}{AC} \\
\end{align}\]
\[\therefore AC=\dfrac{87}{\tan 30}=\dfrac{87}{\dfrac{1}{\sqrt{3}}}\](\[\because \tan 30=\dfrac{1}{\sqrt{3}}\], from trigonometric table)
\[\therefore AC=87\sqrt{3}\]m.
From the figure we can find that,
Ac = AB + BC
\[\begin{align}
& \therefore BC=AC-AB=87\sqrt{3}-\dfrac{87}{\sqrt{3}} \\
& BC=\dfrac{87\times 3-87}{\sqrt{3}}=\dfrac{174}{\sqrt{3}} \\
\end{align}\]
Multiply \[\sqrt{3}\]in numerator and denominator,
\[\dfrac{174\sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\dfrac{174\sqrt{3}}{3}=58\sqrt{3}\]
Hence, \[BC=58\sqrt{3}\]m.
\[\therefore \]The distance travelled by balloon = \[58\sqrt{3}\]m.
Note: The height of the balloon doesn’t change after the time interval. Thus we can calculate the distance travelled, given the initial and final angles of elevation. Remember to subtract the height of the girl from ground, as elevation of the balloon is to be taken from the eye length of the girl.
Complete step-by-step answer:
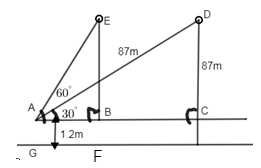
It is given that the height of the girl who sees the balloon is 1.2m. So let us mark the height of the girl from ground G, as AG = 1.2m.
From the figure, AG is parallel to BF i.e. AG || BF.
Hence, AG = BF = 1.2m.
We need to find the distance travelled by the balloon i.e. we need to find the distance BC.

Given that the balloon is at a height of 88.2m from the ground.
\[\therefore EF=88.2\]m
First the girl sees the balloon at an angle of \[{{60}^{\circ }}\]. So from the figure we can say that,
\[\angle EAB={{60}^{\circ }}\]
After the balloon travels to an unknown distance, the girl sees the balloon at an elevation of \[{{30}^{\circ }}\].
\[\therefore \angle DAC={{30}^{\circ }}\]
And the distance travelled by the balloon = BC.
From the figure, we can say that, EF = BE + BF.
\[\begin{align}
& \therefore BE=EF-BF \\
& BE=88.2-1.2=87m \\
\end{align}\]
Hence, BE = DC = 87 m.
From the figure we can say that \[\angle ABE\] and \[\angle ACD\]are right angled.
\[\therefore \angle ABE={{90}^{\circ }}\] and \[\angle ACD={{90}^{\circ }}\].
Let us first consider, \[\vartriangle EAB\], from where we need to find distance AB.
We know, \[\angle EAB={{60}^{\circ }}\]and length of BE = 87m.
\[\tan A\]= Opposite side to angle A / Side adjacent to angle A = \[\dfrac{BE}{AB}\].
\[\tan 60=\dfrac{87}{AB}\Rightarrow AB=\dfrac{87}{\tan {{60}^{\circ }}}\]
From the trigonometric table, we know that \[\tan {{60}^{\circ }}=\sqrt{3}\].
\[\therefore AB=\dfrac{87}{\sqrt{3}}\]m.
Now let us consider, \[\vartriangle DAC\], where DC = 87m and \[\angle DAC={{30}^{\circ }}\].
\[\begin{align}
& \tan 30=\dfrac{DC}{AC} \\
& \Rightarrow \tan 30=\dfrac{87}{AC} \\
\end{align}\]
\[\therefore AC=\dfrac{87}{\tan 30}=\dfrac{87}{\dfrac{1}{\sqrt{3}}}\](\[\because \tan 30=\dfrac{1}{\sqrt{3}}\], from trigonometric table)
\[\therefore AC=87\sqrt{3}\]m.
From the figure we can find that,
Ac = AB + BC
\[\begin{align}
& \therefore BC=AC-AB=87\sqrt{3}-\dfrac{87}{\sqrt{3}} \\
& BC=\dfrac{87\times 3-87}{\sqrt{3}}=\dfrac{174}{\sqrt{3}} \\
\end{align}\]
Multiply \[\sqrt{3}\]in numerator and denominator,
\[\dfrac{174\sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\dfrac{174\sqrt{3}}{3}=58\sqrt{3}\]
Hence, \[BC=58\sqrt{3}\]m.
\[\therefore \]The distance travelled by balloon = \[58\sqrt{3}\]m.
Note: The height of the balloon doesn’t change after the time interval. Thus we can calculate the distance travelled, given the initial and final angles of elevation. Remember to subtract the height of the girl from ground, as elevation of the balloon is to be taken from the eye length of the girl.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




