Question

A $1.15kg$ copper rod rests on two horizontal rails $95cm$ apart and carries a current of $53.2A$ from one rail to the other. The coefficient of static friction is $0.58$. Find the smallest magnetic field (not necessarily vertical) that would cause the bar to slide.
$\begin{align}
  & A)0.112T \\
 & B)115T \\
 & C)120T \\
 & D)135T \\
\end{align}$

Answer 1

Hint: All the forces acting on the copper rod is determined. An expression for the magnetic field is derived by considering all these forces on the copper rod. The angle at which the copper rod should be oriented with the vertical axis is calculated by equating the first differential of the magnetic field with respect to this angle, to zero. Using this value of angle, the smallest magnetic field that would cause the bar to slide is determined.
Formula used:
$1){{F}_{-x}}={{\mu }_{s}}\times {{F}_{z}}$
$2){{F}_{x}}={{F}_{-x}}$
$3)B=\dfrac{{{\mu }_{s}}\times mg}{IL(\cos \theta +{{\mu }_{s}}\sin \theta )}$
\[4)\dfrac{dB}{d\theta }=0\]

Complete answer:
We are provided with a copper rod of mass $1.15kg$resting on two horizontal rails, which are $95cm$ apart. This copper rod is said to carry a current of $53.2A$ from one rail to the other. The coefficient of static friction is taken to be $0.58$. We are required to find the smallest magnetic field (not necessarily vertical) that would cause the bar to slide.
Let us assume that the copper rod is resting along the positive y axis, as shown in the following figure. Clearly, the horizontal rails are kept along the positive x axis. Let us also assume that current in the copper rod is flowing along the positive y axis, as shown. Clearly, this current produces a magnetic field around the copper rod in anticlockwise direction, around the copper rod, using right hand rule. Let us call this magnetic field $B$. This magnetic field in turn exerts a magnetic force on the copper rod, which tends to slide the rod in the positive x-direction. Let us call this magnetic force $f$.

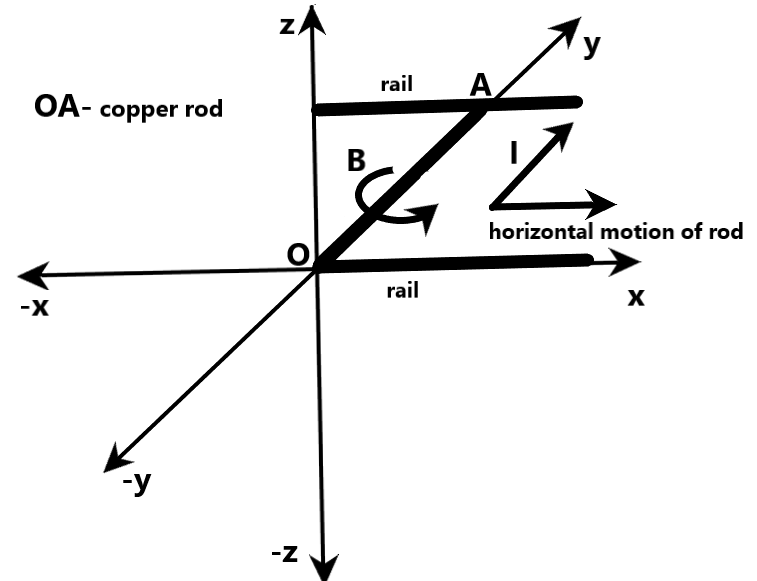
Now, let us consider all the forces acting on the copper rod when current starts flowing through the rod. Clearly, there is force exerted by the rod on the rails due to its weight. If we call this force ${{F}_{-z}}$, then, ${{F}_{-z}}$ is given by
${{F}_{-z}}=mg$
where
${{F}_{-z}}$ is the force exerted by the copper rod on the rail
$m$ is the mass of the rod
$g$ is the acceleration due to gravity
Let this be equation 1. Note that this force acts in the negative z-direction.
When there is force exerted by the rod on the rails due to its weight, there happens to be a normal reactional force acting on the rod exerted by the rails. Let us call this normal reactional force ${{F}_{z}}$. Note that this force acts in the positive z-direction
Now, as already assumed, the magnetic field is going to displace the copper rod in the positive x-direction. Obviously, there is a frictional force acting on the rod, in the negative x-direction. Let us call this frictional force on the rod, ${{F}_{-x}}$. Here, the maximum frictional force acting on the copper rod can be expressed as
${{F}_{-x}}={{\mu }_{s}}\times {{F}_{z}}$
where
${{F}_{-x}}$ is the maximum frictional force acting on the rod when it just begins to slide
${{\mu }_{s}}$ is the coefficient of static friction
${{F}_{z}}$ is the normal force acting on the copper rod in the positive z-direction
Let this be equation 2. Note that this force acts in the negative x-direction because we have assumed that the copper is going to move in the positive x-direction.
Now, if we separate the magnetic field generated in the copper rod into its downward component and eastward component, separate components of magnetic force can also be taken into consideration. If ${{B}_{-z}}$ represents the downward component of magnetic field in the negative z-direction, then, ${{B}_{-z}}$ is given by
${{B}_{-z}}=B\cos \theta $
where
${{B}_{-z}}$ is the downward component of the magnetic field
$B$ is the magnetic field generated due to current flow in the copper rod
$\theta $ is the angle measured from the vertical axis
Let this be equation 3.
Similarly, if ${{B}_{x}}$ represents the eastward component of magnetic field, then, ${{B}_{x}}$ is given by
${{B}_{x}}=B\sin \theta $
where
${{B}_{x}}$ is the eastward component of the magnetic field
$B$ is the magnetic field generated due to current flow in the copper rod
$\theta $ is the angle measured from the vertical axis
Let this be equation 4.
Now, if magnetic force generated due to ${{B}_{-z}}$ is given by ${{f}_{x}}$, then, ${{f}_{x}}$ is given by
${{f}_{x}}=IL{{B}_{-z}}=ILB\cos \theta $
where
${{f}_{x}}$ is the magnetic force component of $f$ generated due the magnetic field component ${{B}_{-z}}$
${{B}_{-z}}=B\cos \theta $, from equation 3
$I$ is the current flowing through the copper rod
$L$is the length of the copper rod
Let this be equation 5. Note that this force acts along the positive x-direction by applying Fleming’s right-hand rule.
Similarly, if magnetic force generated due to ${{B}_{x}}$ is given by ${{f}_{z}}$, then, ${{f}_{z}}$ is given by
${{f}_{z}}=IL{{B}_{x}}=ILB\sin \theta $
where
${{f}_{z}}$ is the magnetic force component of $f$ generated due the magnetic field component ${{B}_{x}}$
${{B}_{x}}=B\sin \theta $, from equation 4
$I$ is the current flowing through the copper rod
$L$is the length of the copper rod
Let this be equation 6. Note that this force acts along the positive z-direction by applying Fleming’s right-hand rule.
Now, considering all the forces on the rod in the z-axis, we have
${{F}_{z}}={{F}_{-z}}-{{f}_{z}}=mg-ILB\sin \theta $
where
${{F}_{z}}$ is the normal reaction force exerted on the copper rod by the rails in the positive z-direction
${{F}_{-z}}=mg$ is the force exerted on the negative z-direction due to the weight of the rod (from equation 1)
${{f}_{z}}$ is the magnetic force on the rod in the positive z- direction, due to magnetic field component ${{B}_{x}}$
Let this be equation 7.
Substituting equation 7 in equation 2, we have
${{F}_{-x}}={{\mu }_{s}}\times {{F}_{z}}={{\mu }_{s}}\times (mg-ILB\sin \theta )$
where
${{F}_{-x}}$ is the frictional force acting on the rod in the negative x-direction
${{\mu }_{s}}$ is the coefficient of static friction
$m$ is the mass of the copper rod
$g$ is the acceleration due to gravity
$I$ is the current flowing through the copper rod
$L$ is the length of the copper rod between the rails
$B\sin \theta $ is the component of magnetic field in the positive x-direction
Let this be equation 8.
Now, when the copper rod just starts sliding in the positive x-direction, the magnetic force along the positive x-direction must be equal to the frictional force acting along the negative x-direction. Therefore, we can equate equation 5 and equation 8 as follows:
${{F}_{x}}={{F}_{-x}}\Rightarrow ILB\cos \theta ={{\mu }_{s}}\times (mg-ILB\sin \theta )$
Let this be equation 9.
Solving for $B$ in equation 9, we have
$ILB\cos \theta ={{\mu }_{s}}\times (mg-ILB\sin \theta )\Rightarrow B=\dfrac{{{\mu }_{s}}\times mg}{IL(\cos \theta +{{\mu }_{s}}\sin \theta )}$
Let this be equation 10.
Now, to find the minimum magnetic field required to make the copper rod start sliding in the horizontal plane, we take the first differential of equation 10 with respect to $\theta $. Clearly, we have
$\dfrac{dB}{d\theta }=0\Rightarrow \dfrac{d\left( \dfrac{{{\mu }_{s}}\times mg}{IL(\cos \theta +{{\mu }_{s}}\sin \theta )} \right)}{d\theta }=0\Rightarrow \dfrac{{{\mu }_{s}}mg({{\mu }_{s}}\cos \theta -\sin \theta )}{IL{{(\cos \theta +{{\mu }_{s}}\sin \theta )}^{2}}}=0\Rightarrow \theta ={{\tan }^{-1}}{{\mu }_{s}}$
Therefore, angle at which the copper road should be oriented with the z-axis is given by
$\theta ={{\tan }^{-1}}{{\mu }_{s}}={{\tan }^{-1}}0.58=30{}^\circ $
where
${{\mu }_{s}}=0.58$ is the coefficient of static friction, as provided in the question
Substituting this value of $\theta $ in equation 10, we have
${{B}_{\min }}=\dfrac{{{\mu }_{s}}\times mg}{IL(\cos \theta +{{\mu }_{s}}\sin \theta )}=\dfrac{0.58\times 1.15\times 9.8}{53.2\times 0.95\times (\cos 30{}^\circ +0.58\times \sin 30{}^\circ )}=\dfrac{6.5366}{50.54\times (0.866+0.29)}=0.112T$
where
${{B}_{\min }}$ is the smallest magnetic field that would cause movement of the copper rod

So, the correct answer is “Option A”.

Note:
Students need to notice that vertical movement of copper is not considered here. Since we are asked to do so, we need to assume horizontal movement of the copper rod from the beginning itself. For easiness, in the above solution, the copper rod is assumed to be sliding in the positive x direction, thereby taking the directions of forces acting on the copper rod accordingly. Also, the subscripts given along with the different forces acting on the copper rod can give a fair idea about the direction of that particular force being considered.