Question

A 110kg panda is riding on a 3.0m long swing whose mass can be considered negligible. The highest point of its arc occurs when the swing makes a ${{20}^{\circ }}$ angle with the vertical.
What is the magnitude of the total tension in the ropes of the swing at that point?
A: 0 N
B: 103 N
C: 369 N
D: 1013 N
E: 1078 N

Answer 1

Hint: This is an example of motion in a vertical circle as the panda completes arcs in the swing. The total tension is the required force here. All the necessary forces can be considered by constructing a free body diagram according to the given criterion.

Step by step answer: We are given that the mass of the panda is 110kg and the highest point of the swing occurs when it forms ${{20}^{\circ }}$with the vertical. With the given conditions, we can construct a free body diagram of the question and identify the forces acting in the system.

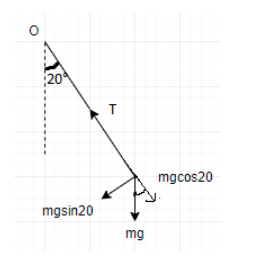
In the free body diagram, we have resolved the gravitational force into its horizontal and vertical components in accordance with the angle $\theta ={{20}^{\circ }}$

From, figure, we can infer that the tension acts opposite to the horizontal component of gravitational force.
Thus,
$
  T=mg\cos 20 \\
 \therefore T=110\times 9.8\times 0.94=1013N \\
$
Hence, option D is the correct answer among the given options.

Note: While solving such questions the most crucial thing is to draw the free body diagram correctly.Free body diagram is defined as a graphical illustration or the representation of all the forces that are applied. It also includes the moments and the resultants. It is helpful to solve both simple and complex problems in mechanics.