Question

A $100cm$ long thin tube (sealed at both ends) lies horizontally, in the middle $0.1m$ containing mercury and the two ends containing air at standard atmospheric pressure. If the tube is turned to a vertical position, by what amount will the mercury be displaced?

Answer 1

Hint: This problem can be solved by using Boyles’ law to find out the change in pressure of the air in the two ends due to the change in their volumes. The pressure in the lower chamber when placed vertically will be equal to the sum of the pressure applied by the mercury and the air in the upper column for equilibrium.

Formula used:
$PV=\text{constant}$

Complete step by step answer:
Let us draw a complete diagram showing the tube in the horizontal and vertical positions.

Now, let us analyze the question.
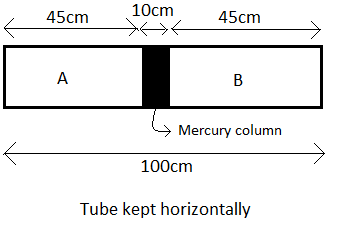
The length of the tube is $100cm$ and it has a $10cm$ column of mercury at the center.
Therefore, the lengths of the two equal chambers A and B, where air at standard atmospheric pressure is present will be $\dfrac{100-10}{2}=\dfrac{90}{2}=45cm$ as shown in the figure.
Let the pressures in the chambers A and B be ${{P}_{A}}$ and ${{P}_{B}}$ respectively.
Now, ${{P}_{A}}={{P}_{B}}=76cm\text{ of Hg}$ --(1) (Since the standard atmospheric pressure is $76cm\text{ of Hg}$)
Let the volumes of these two chambers be ${{V}_{A}}$ and ${{V}_{B}}$ respectively.
Let the area of the cross section of the tube be $A$.
Now, the volume can be written as the product of the cross sectional area and the length.
$\therefore {{V}_{A}}={{V}_{B}}=A\times 45=45A$ --(2)
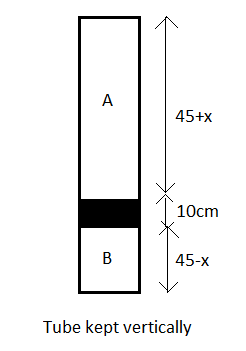
Now, the tube is kept vertically and as shown in the figure, the mercury column shifts downwards by $x\text{ }cm$ due to the effect of gravity.
Therefore, the length of the chambers A and B as now shown in the figure will be $45+x$ and $45-x$ respectively.
Let the new pressure of the air in chamber $A$ be ${{P}_{A}}'$ and that in B be ${{P}_{B}}'$.
The new volumes of the chambers A and B will be ${{V}_{A}}'$ and ${{V}_{B}}'$.
Now, as volume can be written as the product of area and length, we get
${{V}_{A}}'=A\times \left( 45+x \right)$ --(3)
${{V}_{B}}'=A\times \left( 45-x \right)$ --(4)
Now, according to Boyle’ law, the product of the pressure $P$ and the volume $V$ of an ideal gas remains constant.
$\therefore {{P}_{A}}{{V}_{A}}={{P}_{A}}'{{V}_{A}}'=\text{constant}$
$\therefore {{P}_{A}}{{V}_{A}}={{P}_{A}}'{{V}_{A}}'$ --(5)
Similarly,
$\therefore {{P}_{B}}{{V}_{B}}={{P}_{B}}'{{V}_{B}}'=\text{constant}$
$\therefore {{P}_{B}}{{V}_{B}}={{P}_{B}}'{{V}_{B}}'$ --(6)
Now, let us consider (5) for chamber A
${{P}_{A}}{{V}_{A}}={{P}_{A}}'{{V}_{A}}'$
Using (1), (2) and (3) in the above equation, we get
$76\times 45A={{P}_{A}}'\left( 45+x \right)A$
$\therefore {{P}_{A}}'=\dfrac{76\times 45}{45+x}$ --(7)
Similarly or chamber B, we consider (6) and get
${{P}_{B}}{{V}_{B}}={{P}_{B}}'{{V}_{B}}'$
Using (1), (2) and (4) in the above equation, we get
$76\times 45A={{P}_{B}}'\left( 45-x \right)A$
$\therefore {{P}_{B}}'=\dfrac{76\times 45}{45-x}$ --(8)
Now, from the figure of the tube in the vertical position, we see that for the chamber B and thus the whole tube to be in equilibrium, the pressure exerted by the chamber B must be equal to the sum of the pressures applied by the chamber A and the mercury column.
The pressure of the mercury column will be $10cm\text{ of Hg}$.
$\therefore {{P}_{A}}'+10={{P}_{B}}'$ --(9)
Putting (7) and (8) in (9), we get
$\dfrac{76\times 45}{45+x}+10=\dfrac{76\times 45}{45-x}$
$\Rightarrow \dfrac{76\times 45}{45-x}-\dfrac{76\times 45}{45+x}=10$
$\Rightarrow \left( 76\times 45 \right)\left[ \dfrac{1}{45-x}-\dfrac{1}{45+x} \right]=10$
$\Rightarrow \left( 76\times 45 \right)\left[ \dfrac{45+x-\left( 45-x \right)}{\left( 45-x \right)\left( 45+x \right)} \right]=10$
$\Rightarrow \left( 76\times 45 \right)\left[ \dfrac{45+x-45+x}{{{45}^{2}}-{{x}^{2}}} \right]=10$ $\left( \because \left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}} \right)$
$\Rightarrow \left( 76\times 45 \right)\left[ \dfrac{2x}{{{45}^{2}}-{{x}^{2}}} \right]=10$
$\Rightarrow \left( 3420 \right)\left[ 2x \right]=10\left( {{45}^{2}}-{{x}^{2}} \right)$
$\Rightarrow \left( 342 \right)\left( 2x \right)={{45}^{2}}-{{x}^{2}}$
$\Rightarrow 684x=2025-{{x}^{2}}$
$\Rightarrow {{x}^{2}}+684x-2025=0$ --(10)
Now the roots of a quadratic equation of the form $a{{x}^{2}}+bx+c=0$ are given by
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Therefore, using this for (10), we get
$x=\dfrac{-684\pm \sqrt{{{684}^{2}}-4\left( 1 \right)\left( -2025 \right)}}{2\left( 1 \right)}=\dfrac{-684\pm \sqrt{467856+8100}}{2\left( 1 \right)}=\dfrac{-684\pm \sqrt{475956}}{2}$
$\therefore x=\dfrac{-684\pm 689.90}{2}$
In the above equation, we will consider $+689.90$ and not $-689.90$ since we need a positive value of $x$ according to the figure.
$\therefore x=\dfrac{-684+689.90}{2}=\dfrac{5.90}{2}=2.95cm$
Hence, the displacement of the mercury column is by $2.95cm$.

Note:
Students must note and understand that in the horizontal position the mercury was situated perfectly at the centre and remained in that way because the force of gravity was not playing a role in deciding the length of the columns in that case. However, when the tube was kept vertically, the force of gravity started acting on the mercury column which shifted downward until the pressure in the lower chamber became enough to balance the weight of the mercury column and the pressure of the air above it. In the horizontal position, there was no need of balancing each others’ weight by the different columns.