Question

A $1000\,N$ block is placed on an inclined plane with an angle of${30^0}$. Find the components of the weight
(a) parallel
(b) perpendicular to the inclined plane.

Answer 1

Hint:To solve this problem first draw a free body diagram from the given data in the question. A free body diagram is a graphical illustration used to visualize the applied forces, moments, and resulting reactions on a body in a given condition.

Complete step by step answer:
Given; $1000N = mg$, $m = 100kg$ and $g = 10{\text{ }}m/{s^2}$.

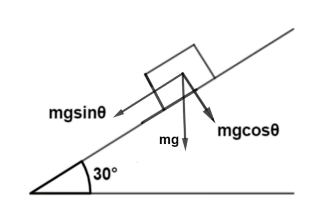
(a) Component of the block parallel to the plane is, $mg\cos \theta $
Component parallel to inclined plane $ = mg\cos \theta $
$ \Rightarrow 100 \times 10 \times \sin {30^0}$
Put the value of $\sin {30^0}$ in the above equation
$ \Rightarrow 1000 \times \dfrac{1}{2}=500$

(b) Component perpendicular to inclined plane $ = mg\sin \theta $
$ \Rightarrow 100 \times 10 \times \cos {30^0}$
Put the value of $\cos {30^0}$ in the above equation
$ \Rightarrow 1000 \times \dfrac{{\sqrt 3 }}{2}=500\sqrt 3 $

Additional information: Sometimes the resultant of the force system is not equal to zero. That means the body is not in equilibrium. The force which is required to keep the body in equilibrium, is known as equilibrant. According to this principle, ‘A body is said to be in equilibrium if the algebraic sum of all forces acting on the body is zero, and also if the algebraic sum of moments of forces about any fixed point is zero. A body is said to be in equilibrium if there is no translation and no rotation of the body under the application of external forces.

Note:A free-body diagram is the diagram which represents the various forces acting on the body. The self-adjusting opposing and resisting friction F which opposes the sliding motion of one body over another, has a limiting value and if the applied force exceeds this value, the body begins to move. This limiting value of the force is called the limiting friction and at this stage the body is in limiting equilibrium and just on the verge of motion.