Question

A 1000 kg engine pulls a train of 4 wagons of 2500 kg each along a horizontal railway track. If the engine exerts the force of 50000 N on wagons and track offers force of friction 2500 N on each wagon, then calculate 1) The net accelerating force. 2) The acceleration of the train. 3) the force of wagon 1 on wagon 2.

Answer 1

Hint: In this question, we have been asked to calculate the net accelerating force, the acceleration of train and the force of wagon 1 on wagon 2. We know that the force is given as mass times acceleration. Therefore, we shall calculate acceleration using Newton’s law. Now, we also know that the friction force opposes motion. Therefore, it will be in the opposite direction of acceleration of the train. Therefore, net force can be given by the difference between the force by engine and the friction force.

Complete step by step answer:
The FBD of the given system can be drawn as shown in the figure below.

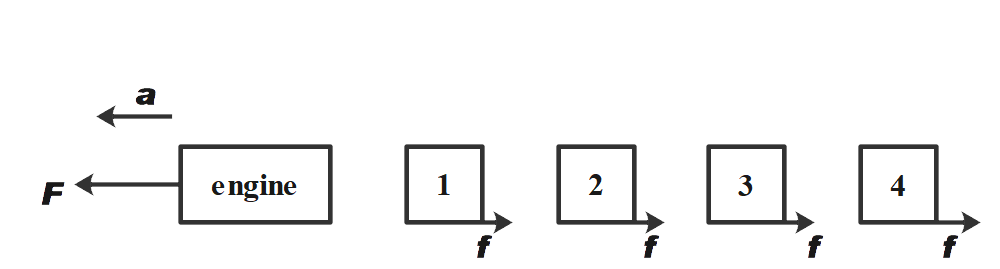
Given that,
Mass of engine \[{{m}_{e}}\] = 1000 kg
Mass of wagon \[{{m}_{w}}\] = 2500 kg each
Force by engine \[F\] = 50000 N
Friction on each wagon \[f\]= 2500 N
Now, we know that the friction force is applied in the opposite direction of acceleration as shown in the figure above. The friction force of 2500 N is applied on each wagon
Therefore, net friction force \[f\] is
\[{{f}_{net}}=2500\times 4\]
Therefore,
\[{{f}_{net}}=10000N\]
Therefore, we know from figure that net force on the system will be given by,
\[{{F}_{net}}=F-{{f}_{net}}\]
After substituting the values
We get,
\[{{F}_{net}}=50000-10000\]
Therefore,
\[{{F}_{net}}=40000N\] ………….. (1)
Now, to calculate the acceleration of train
We know from Newton's law that,
\[F=ma\]
Here, m is the total mass that is the sum of mass of engine and all the four wagons
Therefore,
\[m={{m}_{e}}+4{{m}_{w}}\]
After substituting the given values
We get,
\[m=1000+4\times 2500\]
On solving,
\[m=11000kg\] …………. (2)
Therefore, from (1) and (2) we can say that
\[40000=11000\times a\]
Therefore,
\[a=3.63m/{{s}^{2}}\] ………………… (3)
Now, from the figure we can say that force exerted by the wagon 2, 3 and 4 will be equal to force exerted by wagon 1 on wagon 2.
From (3) we can say that acceleration of all the wagons is 3.63. Now the force exerted by wagon 1 on wagon 2 can be given by,
\[{{F}_{12}}=3\times {{m}_{w}}\times a\] ……………. (since force by wagon 1 on 2 will equal force by other wagons on 1)
Therefore,
\[{{F}_{12}}=3\times 2500\times 3.63\]
Therefore,
\[{{F}_{12}}=27225N\]

Note:
From the three laws given by Newton, the second law states that force acting on an object is equal to the product of mass of the object and the acceleration of the same object. Therefore, if the object has a greater mass, greater force will be required to move or accelerate the object. This law can also be stated as the force acting on an object is given as the mass times rate of change of velocity of the object.