Question

A 10 kg wt is suspended as shown below then tension $T_1$ & $T_2$ are​

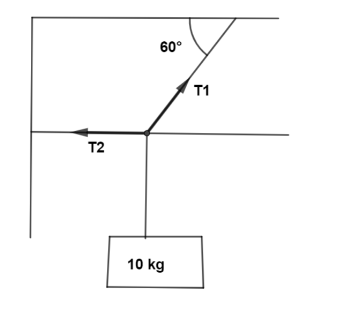
Answer 1

Hint:Redraw the figure and also draw a free body diagram of the body. Using the concept of lami's theorem. To solve this problem, we need to have a clear idea of Lami’s Theorem. According to this theorem when 3 forces are acting at a point and they are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.

Complete step by step answer:

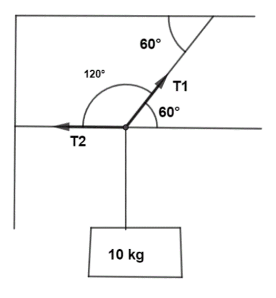
Free body diagram

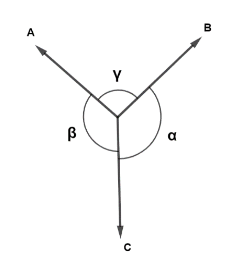
$\dfrac{A}{{\sin \alpha }} = \dfrac{B}{{\sin \beta }} = \dfrac{C}{{\sin \gamma }}{\text{ - - - - - - - - - - - LAMI'S THEOREM}}$

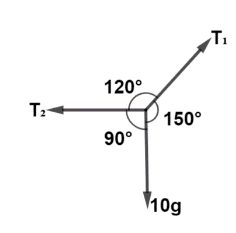
Here,
$\dfrac{{{T_1}}}{{\sin 90}} = \dfrac{{{T_2}}}{{\sin 150}} = \dfrac{{10g}}{{\sin 120}}$
From above relation we get,
${T_1} = 2{T_2} = \dfrac{{10g \times 2}}{{\sqrt 3 }}$
So again from lami's theorem we can find the value of ${T_2}$
$\therefore 2{T_2} = \dfrac{{2 \times 10}}{{\sqrt 3 }}gN$
So, the required answers are
$ \Rightarrow {T_2} = \dfrac{{10}}{{\sqrt 3 }}kg - \omega t$
$ \therefore {T_1} = \dfrac{{20}}{{\sqrt 3 }}kg - \omega t$

Additional information:In physics, Lami's theorem is an equation relating the magnitudes of three coplanar, concurrent and non-collinear vectors, which keeps an object in static equilibrium, with the angles directly opposite to the corresponding vectors. Lami’s theorem is useful for determining the magnitude of unknown forces for a given system.

With this theorem, the property of 3 forces in equilibrium is considered to be a very neat method of solving any kind of three-force problem. If we know the angles between pairs of forces the best method to find these out is Lami’s theorem. The 3 forces should be inward or outward and opposite. Lami's theorem is applied in static analysis of mechanical and structural systems. The theorem is named after Bernard Lamy.

Note:Students should be careful while drawing the free body diagram and the most common mistakes that occur in this type of questions is while drawing free body diagrams and while taking the angle between the forces. DiagramApplication of Lami’s Theorem The derivation of this theorem is from the Sine rule of triangles. In a free body diagram if we represent the forces as lines and translate them in such a way that one head touches the tail of another then we will notice that if the 3 forces are supposed to cancel each other then they will resultantly form a triangle.