Question

A 10 cm long pin lies along the principal axis of a convex lens of focal length 10cm such that the nearer end of the pin is at a distance of 15 cm from the lens. Find the length of the image of the pin formed by the lens.

Answer 1

Hint: By using the lens formula and understanding the concept of its functions of keeping an object and forming an image of it. As the signs are different for components in concave and convex lenses so, we will use them carefully. Since only a convex lens is used here, we will use its facts only by considering two ends of the pins differently so that there will be two objects in front of the lens.

Formula used:
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ where f is called focal length, u is the distance of object and v is the distance of image, $Objec{{t}_{1}}-Objec{{t}_{2}}$

Complete answer:
We will apply here the lens formula $\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ where f is called focal length, u is the distance of object and v is the distance of image.
Focal length: The focal length is always carried out as a distance between principal focus and the optical center of the lens. It can be any lens either convex or concave. Here we have used f as a focal length.
Distance of object: We measure it by taking the distance between the optical center of the lens and the object. Here we have denoted it with the symbol u.
Distance of image: Similar to the distance of an object, we measure it by considering the distance of image from optical center. We will use v for denoting the distance of image formed by the lens.
The diagram with the given conditions in the question has been drawn below.

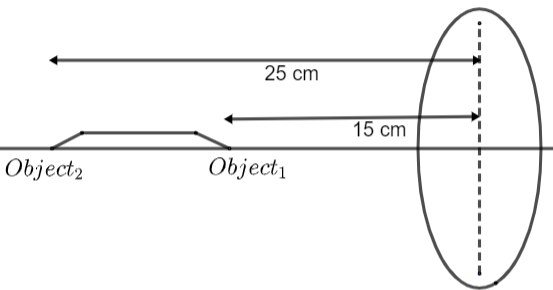
The focal length will be f = + 10, and u = - 15 for the end nearer to the lens and u = - 25 will be for the end of the pin opposite to the lens. By the diagram and values given to us we can calculate the following.

$\begin{align}
  & \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} \\
 & \Rightarrow \dfrac{1}{+10}=\dfrac{1}{v}-\dfrac{1}{-15} \\
 & \Rightarrow \dfrac{1}{v}=\dfrac{1}{+10}+\dfrac{1}{-15} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{3-2}{30} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{1}{30} \\
\end{align}$
So, the image formed by $Objec{{t}_{1}}$ is 30 cm.

Similarly,

$\begin{align}
  & \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} \\
 & \Rightarrow \dfrac{1}{+10}=\dfrac{1}{v}-\dfrac{1}{-25} \\
 & \Rightarrow \dfrac{1}{v}=\dfrac{1}{+10}+\dfrac{1}{-25} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{5-2}{50} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{3}{50} \\
\end{align}$

Thus, the image formed by $Objec{{t}_{2}}$ is $\dfrac{50}{3}cm$.
Therefore, the total length of the image of the pin will be the distance of the image of $Objec{{t}_{1}}-Objec{{t}_{2}}$.
$\begin{align}
  & 30-\dfrac{50}{3}=\dfrac{90-50}{3} \\
 & \Rightarrow \dfrac{40}{3}=13.4 \\
\end{align}$
Hence, the required total length is 13.4 cm.

Note:
The signs in the values of u, v and f are added by considering the following points:
(1) If a virtual image is formed then v will be negative.
(2) If a real image is formed by the lens, then we will take v as positive.
(3) We are going to take u with a negative sign because we will always find it on the left side of the lens.
(4) If we are considering a convex lens then, we will take focal length f as positive otherwise; in case of concave lens we will take f as negative.