Question

A 10 cm deep well diameter 6cm is dug and the earth spread even to form a platform $22{\text{ cm}} \times {\text{10 cm}} \times {\text{xcm}}$. The value of ‘x’ is
A. 2.2
B. 1.12
C. 1.28
D. 1.3

Answer 1

Hint: First step is to draw the diagram of a cylindrical well and mark its dimension. After this, calculate the volume of the cylinder. This will give the volume of earth dug out. Now calculate the volume of the given cuboid in terms of ‘x’. Finally equate the volume of earth and volume of cuboid.

Complete step-by-step answer:

The diagram is given below:

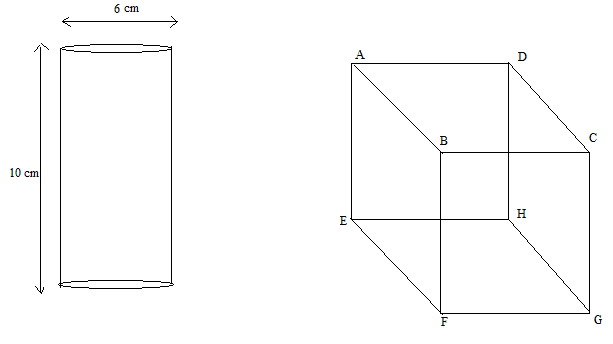
The cylindrical well has diameter = 6cm and height =10cm.

For cuboidal platform, the dimensions are:

EF = 22 cm, FG= 10 cm and FB = x cm.


We know that the volume of cylinder is given as:

Volume = $\pi {{\text{r}}^2}h{\text{ }}$. (1)

The volume of cylinder = Volume of earth dug out.

Putting the values in equation 1, we get:

Volume of earth dug out = $\pi \times {{\text{(3)}}^2} \times 10{\text{
c}}{{\text{m}}^3} = 282.6{\text{c}}{{\text{m}}^3}$.

Now the volume of the cuboidal platform that is formed from earth will be equal to
the volume of earth dug out which in turn is equal to the volume of the cylinder.

$\therefore $ Volume of cuboidal platform = volume of earth dug out

$

   \Rightarrow 22 \times 10 \times {\text{x = 282}}{\text{.6}} \\

   \Rightarrow {\text{x = }}\dfrac{{282.6}}{{220}} = 1.28 \\

 $

Therefore, option C is correct.

Note: In this type of question where one 3D shape is converted to another 3D shape, the volume remains constant i.e. initial volume will be equal to final volume. In this particular question, you should remember the volume of the cylinder and cuboid.