
A
Answer
495.6k+ views
1 likes
Hint: When a ball is suspended by a thread, it acts like a pendulum. When the particle is at a mean position, its potential energy is zero, kinetic energy is maximum , but kinetic energy is zero. Work done by a ball is due to work done by gravity which is given by potential energy.
Use the work energy theorem, according to which change in kinetic energy is equal to work done and work done is equal to potential energy. It means change in potential energy is equal to change in kinetic energy.
And we can calculate velocity at the lowest point.
Formula used: Work done due to gravity
By work energy theorem
Here
Complete step by step solution
We have a blue suspended by a thread.
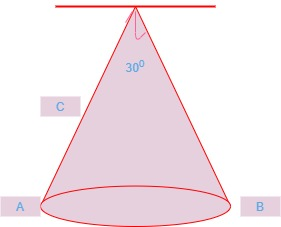
Mass of ball is given by
Since
Here, thread is at
Height through which ball is raised,
Work done due to gravity is given by
By work energy theorem,
According to this, the work done by all forces acting on a particle equals change in the K.E of the particle.
Hence work done by ball is
And velocity at lowest point is
Note
Work energy theorem: The work done by the net force on a particle is equal to the change in the particle's kinetic energy.
The work energy theorem can be derived from Newton's second law: kinetic energy is directly proportional to the mass of the object and to the square of its velocity.
Potential energy is energy an object has because of its position relative to the same other object.
The formula of potential energy depends on the force acting on two objects.
Use the work energy theorem, according to which change in kinetic energy is equal to work done and work done is equal to potential energy. It means change in potential energy is equal to change in kinetic energy.
And we can calculate velocity at the lowest point.
Formula used: Work done due to gravity
By work energy theorem
Here
Complete step by step solution
We have a blue suspended by a thread.

Mass of ball is given by
Since
Here, thread is at
Height through which ball is raised,
Work done due to gravity is given by
By work energy theorem,
According to this, the work done by all forces acting on a particle equals change in the K.E of the particle.
Hence work done by ball is
And velocity at lowest point is
Note
Work energy theorem: The work done by the net force on a particle is equal to the change in the particle's kinetic energy.
The work energy theorem can be derived from Newton's second law: kinetic energy is directly proportional to the mass of the object and to the square of its velocity.
Potential energy is energy an object has because of its position relative to the same other object.
The formula of potential energy depends on the force acting on two objects.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




