Question

A (0, a) and B (0, b), a, b > 0 are two vertices of a triangle ABC where the vertex C (x, 0) is a variable. The value of x when the angle ∠ACB is maximum is?
\[ {\text{A}}{\text{. }}\dfrac{{{\text{a + b}}}}{2} \\
  {\text{B}}{\text{. }}\sqrt {{\text{ab}}} \\
  {\text{C}}{\text{. }}\dfrac{{2{\text{a}}}}{{{\text{a + b}}}} \\
  {\text{D}}{\text{. }}\dfrac{{{\text{ab}}}}{{{\text{a + b}}}} \\ \]

Answer 1

Hint: To find the value of x when the angle ACB is maximum, we use the given coordinates of the points A and B and find the slope of the line from A and B to the point C. Then we apply the formula of the angle between two lines using the slopes of lines AC and BC. Take the maximum value of the angle.

Complete step-by-step solution:

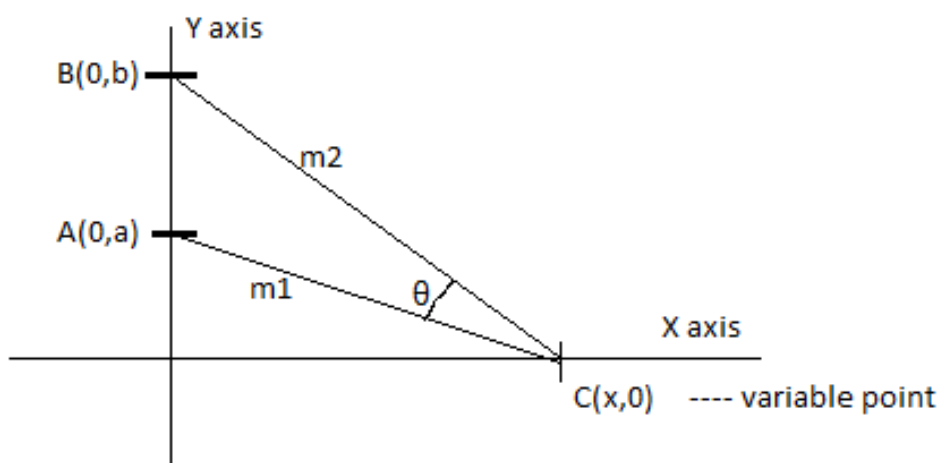
Given Data,
A (0, a) and B (0. b) and C (x, 0)
Let us construct an appropriate figure showing the given data, for our reference.
Now the slope between two points with coordinates (p, q) and (r, s) is given by the formula,
Slope: ${\text{m = }}\dfrac{{{\text{s - q}}}}{{{\text{r - p}}}}$.
Now the slope of the line AC with coordinates (0, a) and (x, 0) is given by
${{\text{m}}_1}{\text{ = }}\dfrac{{{\text{0 - a}}}}{{{\text{x - 0}}}} = - \dfrac{{\text{a}}}{{\text{x}}}$
Now the slope of the line BC with coordinates (0, b) and (x, 0) is given by
${{\text{m}}_2}{\text{ = }}\dfrac{{{\text{0 - b}}}}{{{\text{x - 0}}}} = - \dfrac{{\text{b}}}{{\text{x}}}$
We know the angle between two lines with respective slopes is given by the formula,
${\text{Tan }}\theta {\text{ = |}}\dfrac{{{{\text{m}}_2} - {{\text{m}}_1}}}{{1 + {{\text{m}}_1}{{\text{m}}_2}}}{\text{|}}$, where θ is the angle between the two lines and ${{\text{m}}_1}$and ${{\text{m}}_2}$are the slopes of the respective lines.
Now let the angle between the lines AC and BC be θ, which is given by
$\Rightarrow {\text{Tan }}\theta {\text{ = }}\left| {\dfrac{{ - \dfrac{{\text{b}}}{{\text{x}}}{\text{ + }}\dfrac{{\text{a}}}{{\text{x}}}}}{{1 + \dfrac{{{\text{ab}}}}{{{{\text{x}}^2}}}}}} \right| \\
\Rightarrow {\text{Tan }}\theta {\text{ = }}\left| {{\text{a - b}}} \right|\left| {\dfrac{1}{{{\text{x}} + \dfrac{{{\text{ab}}}}{{\text{x}}}}}} \right| \\ $
Now the angle θ is maximum only when the denominator of this term is the minimum.
For the term,${\text{x}} + \dfrac{{{\text{ab}}}}{{\text{x}}}$ we know AM ≥ GM
$\Rightarrow {\text{x = }}\dfrac{{{\text{ab}}}}{{\text{x}}} \\
   \Rightarrow {{\text{x}}^2}{\text{ = ab}} \\
   \Rightarrow {\text{x = }}\sqrt {{\text{ab}}} \\ $
The value of x when the angle ∠ACB is maximum is$\sqrt {{\text{ab}}} $.
Option B is the correct answer.

Note: In order to solve this type of question the key is to know the formula of relevant geometrical identities like the slope of a line with two-point coordinates, the angle between two lines, etc.
The most important step is to know that the value of the angle between two lines is maximum when the denominator is minimum. Since the Tan function’s value of an angle is directly proportional to its angle, the more the value of the Tan function, the maximum the angle is.
Any value inside the modulus function represented by | | only gives us the positive value of that function.