Question

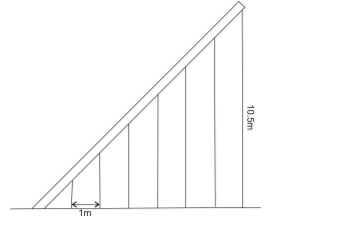
$ 7 $ pillars are used to hold a slant iron gutter as shown in the figure. If the distance between every two pillars is $ 1m $ and height of the last pillar is $ 10.5m $ .Find the height of the first pillar.

Answer 1

Hint: We can easily find the problem of this solution by taking arrangement of pillars equivalent to arithmetic progression (A.P.) problem. In which height of first pillar will represent as ‘a’ and number of pillars represent value of ‘n’ and height of last pillar will either equal to nth term of A.P. or taken as last term(l) of A.P. Then finally using given values in the nth term formula of A.P. to find the required solution of the problem.
Last term or nth term in arithmetic progression (A.P.): $ l = a + \left( {n - 1} \right)d\,\,\,\,or\,\,{T_n} = a + \left( {n - 1} \right)d $ , where ‘a’ is the first term, ‘d’ is the common difference and ‘l’ is last term of the arithmetic

Complete step-by-step answer:

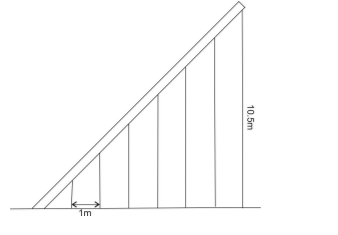
From above it is very clear that arrangement is equivalent to an arithmetic progression problem.

Here, distance between two pillars is equivalent to the common difference of arithmetic progression.
 $ \therefore d = 1 $
Also, the last pillar will act as the last term of the arithmetic progression.
 $ \therefore l = 10.5 $
Since, there are $ 7 $ pillars in arrangements. So, the last pillar will act as either the last term of an arithmetic progression or the seventh term of the arithmetic progression.
Hence, from above we have:
 $ {T_7} = a + \left( {7 - 1} \right)d $
 $ \Rightarrow {T_7} = a + 6d $
Substituting values in above. We have,
 $
  10.5 = a + 6(1) \\
   \Rightarrow 10.5 = a + 6 \\
   \Rightarrow 10.5 - 6 = a \\
   \Rightarrow a = 4.5 \;
  $
Therefore, from above we see that the height of the first pillar is $ 4.5m $ .

Note: Whenever different terms are arranged in such a manner that the distance between each of them are the same. Therefore, the problem is equivalent to an arithmetic progression. Also, for an A.P. last term may be taken as nth term. So, one can use either the formula of nth term or last term to get the required solution of the problem.