Question

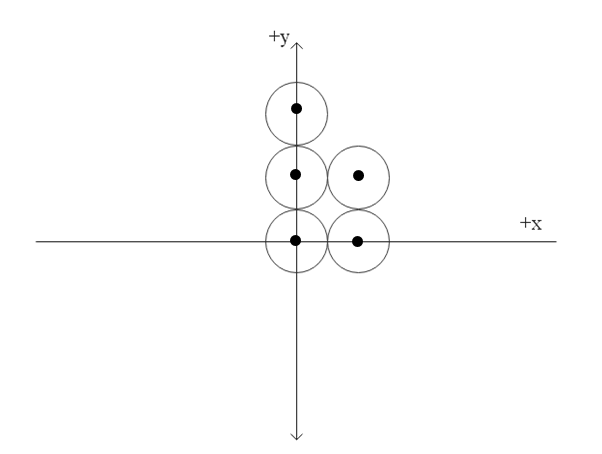
5 uniform circular plates, each of diameter $b$ and mass $m$, are laid out in a pattern shown. Using the origin shown, find the $y$-coordinate of the centre of mass of the five-plate system.

Answer 1

Hint: The system can be considered as a set of 5 point objects of mass $m$ instead of 5 different discs. These point objects will have the same mass as the disc and will lie at the centre of the discs.

Formula used:
Coordinates of the centre of mass (C.O.M.) are given as:
$\Rightarrow {y_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}$ where ${y_{COM}}$ is the $y$ coordinate of the centre of mass, ${y_i}$ and ${m_i}$ are the $y$-coordinate and mass of the ith object, respectively.

Complete step by step solution:
The system that we’ve been given can be replaced with a system of 5 point objects of mass $m$ that have the coordinates of the geometric centres of the discs.Considering the disc as circles, their geometric centres are the centres of the circles and we can then denote the entire disc by a point object that has a mass $m$ and the same coordinates as the centre of the discs.
Given that the diameter of disc is $b$, the coordinates of the point objects can be deducted from the geometry of the pattern as:
$\Rightarrow ({x_1},{y_1}) = (0,0)$
$\Rightarrow ({x_2},{y_2}) = (b,0)$
$\Rightarrow ({x_3},{y_3}) = (0,b)$
$\Rightarrow ({x_4},{y_4}) = (b,b)$
$\Rightarrow ({x_5},{y_5}) = (0,2b)$
Then the $y$-coordinate of the centre of mass can be determined as:
$\Rightarrow {y_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} = \dfrac{{m({y_1}) + m({y_2}) + m({y_3}) + m({y_4}) + m({y_5})}}{{5m}} $
$\Rightarrow \dfrac{{m(0) + m(0) + m(b) + m(b) + m(2b)}}{{5m}} $
$\Rightarrow \dfrac{{4mb}}{{5m}} $
$\Rightarrow \dfrac{{4b}}{5} $
Hence, the centre of mass of the system will have $y$-coordinate equal to $\dfrac{{4b}}{5}$.

Note:
Unless mentioned in the question, the discs can be assumed to have uniform density and hence their centre of mass will be their geometric centre so we do not need to treat each disc individually and find their centre of mass. We should also be careful that we’ve been given the diameter of discs in the question as $b$ and not the radius.