Question

How should 5 capacitors each of capacitance $1\mu F$ be connected so as to produce a total capacitance of $\dfrac{3}{7}\mu F$?

Answer 1

Hint: Capacitors can be connected in combinations in two ways; series and parallel. Select the number of capacitors to be connected in series and the number of capacitors in parallel individually and then connect their equivalent into a combination which gives the required capacitance.

Formula Used:
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......\dfrac{1}{{{C}_{n}}}$
${{C}_{eq}}={{C}_{1}}+{{C}_{2}}+......{{C}_{n}}$

Complete step-by-step solution:
The capacitance of a conductor is its ability to store charge on it. Its SI unit is farad ($F$).
There are two ways to connect capacitors in combinations; series and parallel combinations
In series combination, the reciprocals of the capacitance get added. The equivalent capacitance is smaller than the smallest value.
$\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......\dfrac{1}{{{C}_{n}}}$

In parallel combination, capacitance gets simply added. The equivalent capacitance is larger than the largest value.
${{C}_{eq}}={{C}_{1}}+{{C}_{2}}+......{{C}_{n}}$

In order to get an equivalence of $\dfrac{3}{7}\mu F$, first we can add two capacitors in series, their equivalence will be-

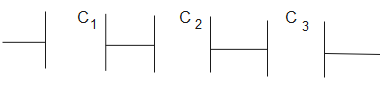
$\dfrac{1}{C}=1+1$
$\therefore C=\dfrac{1}{2}$ - (1)

The remaining set of capacitors can be connected in parallel, their equivalence will be-

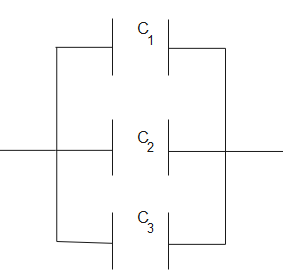
$C'=1+1+1$
$\therefore C'=3$ - (2)
The first set of capacitors connected in series and the second set of capacitors connected in parallel can now be connected in series giving a new equivalent as-
$\begin{align}
  & \dfrac{1}{C''}=\dfrac{1}{\dfrac{1}{2}}+\dfrac{1}{3} \\
 & \Rightarrow \dfrac{1}{C''}=2+\dfrac{1}{3} \\
 & \Rightarrow \dfrac{1}{C''}=\dfrac{7}{3} \\
\end{align}$
$\therefore C''=\dfrac{3}{7}$

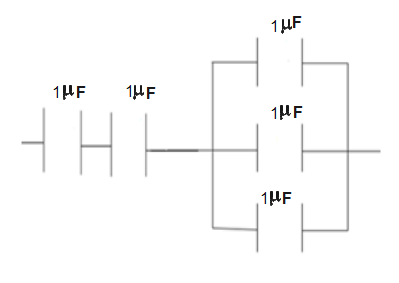
(Each capacitor is of $1\mu F$)

Additional information:
When capacitors are being charged, charge is being stored on their plates and it takes them $t=\infty $ to get charged. When a capacitor is fully charged, the arm in which the capacitor is connected is assumed to have been short-circuited. Half of the total work done by the battery is stored as energy in the capacitor whereas half of it is dissipated as heat.

Note:
Capacitors are devices used to store electrical energy in the presence of an electrical field. Combinations in capacitors are analogous to combinations in resistors. The capacitance of a conductor depends on the permeability of space inside the capacitor, area of cross section and distance between the plates.