Question

35 students like either tea or coffee or both. 25 students like both. How many students like exactly one drink?
A.15
B.18
C.20
D.10

Answer 1

Hint: In this question the number the number of students who like both the tea and the coffee is given and also the number of students who like both the tea and the coffee is given so we will plot these given data in the Venn diagram and then from the Venn diagram we will find the number of students liking either tea or the coffee.

Complete step-by-step answer:
Number of students liking either tea or coffee or both \[ = 35\]
Number of students liking both tea and coffee\[ = 25\]
Now let’s represent this on the Venn diagram

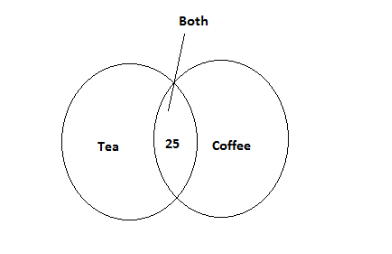
According to the question, we can write
\[n\left( {T \cup C} \right) = 35\] and \[n\left( {T \cap C} \right) = 25\]
Now we have to find the number of students who likes only one drink, i.e. \[n\left( T \right)\]or \[n\left( C \right)\]
So the number of students who like only one drink will be given by the difference in the number of students who like either tea or coffee and the number of students who likes both tea and coffee. Mathematically, \[n\left( {T{\text{ }}or{\text{ }}C} \right) = n\left( {T \cup C} \right) - n\left( {T \cap C} \right)\] where, \[n\left( {T \cup C} \right) = 35\] is the number of students who likes either tea or coffee and \[n\left( {T \cap C} \right) = 25\] is the number of students who likes both tea and coffee.
So, substituting the values in the equation
\[\Rightarrow n\left( {T{\text{ }}or{\text{ }}C} \right) = n\left( {T \cup C} \right) - n\left( {T \cap C} \right)\], we get
\[
\Rightarrow n\left( {T{\text{ }}or{\text{ }}C} \right) = n\left( {T \cup C} \right) - n\left( {T \cap C} \right) \\
   = 35 - 25 \\
   = 10 \;
 \]
Hence the number of student who like only one drink\[ = 10\]
So, the correct answer is “Option D”.

Note: Two events are said to be mutually exclusive when the occurrence of one doesn’t affect the occurrence of another event. Union between the events indicates the summation of the events while the intersection between the events signifies the common values between the events.
 \[P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)\] where, A and B are two mutually exclusive independent events.