Question

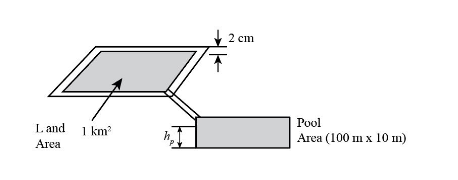
$ 2\;{\rm{cm}} $ of rain has fallen on a square kilometer of land. Assuming that $ 50\% $ of the rain drops could have been collected and contained in a pool having a $ 100\;{\rm{m}} \times {\rm{10}}\;{\rm{m}} $ base, by what level would the water level in the pool have increased?

Answer 1

Hint: In this question, we have to calculate the change in the level of water of land if $ 50\% $ of the rainwater is collected in a pool. The units given for the area and the height are different, so first, we convert all the units into Metric units.
The conversion formulas are given by-
 $
1{\rm{ kilometer = 1000 meter}}\\
1{\rm{ }}{\left( {{\rm{kilometer}}} \right)^2} = {\left( {1000{\rm{meter}}} \right)^2}\\
1{\rm{ centimeter = }}\dfrac{1}{{100}}{\rm{ meter}}
$

Complete step-by-step answer:
The area of the land is,
 $
\Rightarrow A = {\left( {1\;{\rm{km}}} \right)^2}\\
 = {\left( {1000\;{\rm{m}}} \right)^2}
$
The height of the fallen rain on the land is,
 $
\Rightarrow h = 2\;{\rm{cm}}\\
{\rm{ = 0}}{\rm{.02}}\;{\rm{m}}
$
The area of the pool base is,
\[
\Rightarrow {A_p} = 100\;{\rm{m}} \times 10\;{\rm{m}}\\
 = 1000\;{{\rm{m}}^2}
\]

The total volume of the rain falling on the land is given by,
 $
\Rightarrow V = {\text{ The area of the land }} \times {\text{ The height of the fallen rain on the land}}\\
 = A \times h
$
Substituting the values of $ A $ and $ h $ in the equation we get,
 $\Rightarrow V = {1000^2}\;{{\rm{m}}^{\rm{2}}} \times {\rm{0}}{\rm{.02}}\;{\rm{m}} $
Solving this we get,
 $ V = 20000\;{{\rm{m}}^3} $

Now according to the question $ 50\% $ of the total volume of rain is collected and contained in the pool, so
The volume of the rain water collected in the pool is,
 $\Rightarrow {V_p} = 0.5 \times V $
Substituting the value of $ V $ in the equation we get,
 $
\Rightarrow {V_p} = 0.5 \times 20000\;{{\rm{m}}^3}\\
\Rightarrow {V_p} = 10000\;{{\rm{m}}^3}
$
Let us suppose the level of the water in the pool be $ {h_p} $ then,
\[\Rightarrow {\text{The increase in the level of water in the pool = }}\dfrac{{{\text{The volume of the rain water collected in the pool}}}}{{{\text{The area of pool base}}}}\]
Or,
 $\Rightarrow {h_p} = \dfrac{{{V_p}}}{{{A_p}}} $
Substituting the values of $ {V_p} {\text{ and } }{A_p} $ in the equation we get,
 $
\Rightarrow {h_p} = \dfrac{{10000\;{{\rm{m}}^3}}}{{1000\;{{\rm{m}}^2}}}\\
\Rightarrow {h_p} = 10\;{\rm{m}}
$

Therefore, the increase in the water level in the pool is $ 10{\rm{m}} $ .

Note: It should be noted that while working with different units, the first step should be to convert all the relevant units to Metric Units. The most commonly used Metric units are as following-
(i) Metre for Length or Distance
(ii) Second for Time
(iii) Kilogram for Mass