Question

Where do $2$ perpendicular lines intersect?

Answer 1

Hint: The slopes of two perpendicular lines are related by the equation \[{{m}_{1}}{{m}_{2}}=-1\]. From this, we can show that the slopes of two perpendicular lines can never be equal and therefore they must intersect. To answer the above question, we need to consider two perpendicular lines, say ${{L}_{1}}$ and ${{L}_{2}}$. By terminating both of the lines ${{L}_{1}}$ and ${{L}_{2}}$ at the point of intersection, we will have one case. And by not terminating them at the intersecting point, we will have the other case.

Complete step by step solution:
Let us consider two lines ${{L}_{1}}$ and ${{L}_{2}}$, which are perpendicular to each other. We know that the slopes of two perpendicular lines are related such that their product is equal to the negative of one, that is, $-1$. So if the slope of the first line ${{L}_{1}}$ is equal to \[{{m}_{1}}\] and that of the second line ${{L}_{2}}$ is equal to ${{m}_{2}}$, then these can be related by the below equation
\[\begin{align}
  & \Rightarrow {{m}_{1}}{{m}_{2}}=-1 \\
 & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{2}}} \\
\end{align}\]
Clearly, from the above equation we can say that two perpendicular lines can never have equal slopes. And we know that two lines having unequal slopes do intersect each other at a point.
Now, the intersection of two perpendicular lines can have two cases. For this, let us represent these two perpendicular lines ${{L}_{1}}$ and ${{L}_{2}}$ in the below figure.

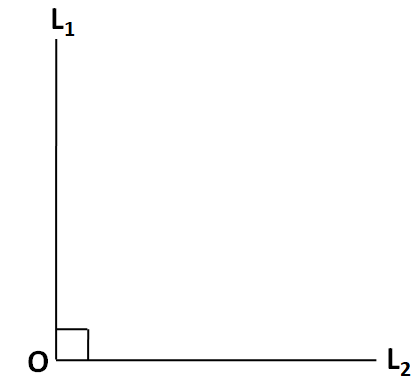
In the above figure, we can see that the two perpendicular lines ${{L}_{1}}$ and ${{L}_{2}}$ are intersecting at the point O. The two lines are forming a corner at the point O, since they are terminating at the point O.
From the definition of a line, we know that a line is not of a finite length. Therefore, it is not necessary that the two lines ${{L}_{1}}$ and ${{L}_{2}}$ must terminate at O. They can also extend beyond O infinitely, as shown in the below figure.

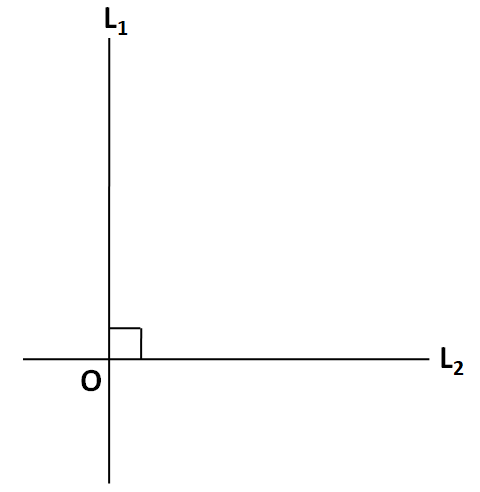
Hence, from the above two cases considered, we can conclude that two perpendicular liens can either terminate at the intersection point to form a corner, or they can continue their respective paths after getting intersected.

Note: It is necessary to show mathematically that the two perpendicular lines can never have equal slopes by using the condition \[{{m}_{1}}{{m}_{2}}=-1\]. Do not get confused that we have opposed the infinite length definition of the line in the first case considered above, where the two lines terminate at the point O. They are still infinitely long, since their initial point is not labeled in the first figure.