Question

2( lb+bh+hl) is formula of: -
(a) Area of cuboid
(b) Area of cube
(c) Volume of cuboid
(d) None of these

Answer 1

Hint: Assume l, b, and h as the length, breadth, and height of a 3 – dimensional shape. Consider each option one – by – one and draw their diagram with the labeling of their dimensions. Check these options and find the expression for their area and volume, whichever physical quantity is asked, to get the correct answer.

Complete step-by-step solution
Here, we have been provided with a formula: - \[2\left( lb+bh+hl \right)\] and we have to determine the shape and the physical quantity (area, volume, etc) from the given options.
Now, let us assume l, b, and h as the length, breadth, and height of the required shape. Let us consider each option one – by – one.
(a) Area of cuboid
So, here we have to check if the provided formula is the formula for the area of cuboid or not. A cuboid is shown below: -

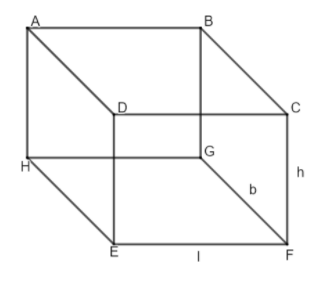
A cuboid has 6 faces made up of 6 rectangles. Two rectangles have dimensions l, b; two have b, h, and two have h, l. So, the total area of a cuboid will be the total area of these 6 rectangles.
\[\Rightarrow \] Area = [Ar. (ABCD) + Ar. (EFGH)] + [Ar. (ADEH) + Ar. (BCFG)] + [Ar. (CDEF) + Ar.(ABGH)]
\[\Rightarrow \] Area = (l \[\times \] b + l \[\times \] b) + (b \[\times \] h + b \[\times \] h) + (l \[\times \] h + l \[\times \] h)
\[\Rightarrow \] Area = 2lb + 2bh + 2hl
\[\Rightarrow \] Area = 2 (lb + bh + hl)
Hence, option (a) is correct.
(b) Area of a cube
The diagram of a cube can be shown as: -

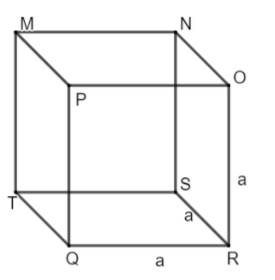
A cube consists of 6 faces and all of them are squares. So, there cannot be three different dimensions for length, breadth, and height for a cube. Here, the area is the sum of the area of all 6 squares.
\[\Rightarrow \] Area = \[{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}\]
 \[\Rightarrow \] Area = \[6{{a}^{2}}\]
Hence, option (b) is incorrect.
(c) Volume of a cuboid
We know that volume of any shape is the product of its base area and height. So, considering the same cuboid used in option (a), we have,

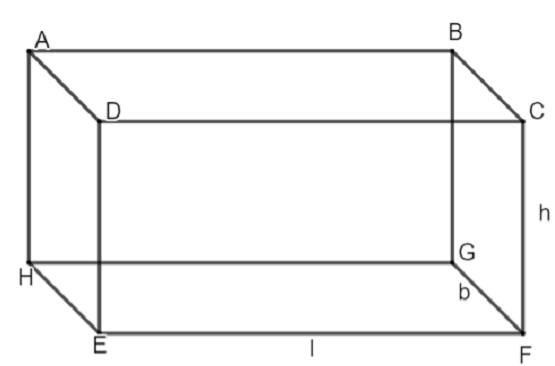
Here, EFGH is considered as the base of the cuboid. So, the area of the base can be given as: -
\[\Rightarrow \] Area = l \[\times \] b
Therefore, the volume relation is: -
\[\Rightarrow \] Volume = Area of base \[\times \] height
\[\Rightarrow \] Volume = l \[\times \] b \[\times \] h
\[\Rightarrow \] Volume = lbh
Hence, the option (c) is incorrect.
On checking all the options, we can conclude that our answer is an option (a).

Note: Note: One may note that we have eliminated the options one by one to get the correct one. You can also remember the area and volume relations of different and basic 3 – D objects, like the cube, cuboid, cylinder, cone, etc, to directly choose the correct option. Remember that a cuboid can be converted into a cube if its length = breadth = height. One important thing to note is that we have been provided with the term ‘area’ in the first two options, so we have to consider it as the total surface area and not the lateral surface area.