
1L of a gas is at a pressure of \[{{10}^{-6}}\]of Hg at \[{{25}^{o}}C\]. How many molecules are present?
(A)- \[3.2\times {{10}^{6}}\]
(B)- \[3.2\times {{10}^{13}}\]
(C)- \[3.2\times {{10}^{10}}\]
(D)- \[3\times {{10}^{4}}\]
Answer
596.4k+ views
Hint: We can calculate the number of molecules using the ideal gas equation. In the above question we are given the pressure, volume and temperature of the gas.
\[PV=nRT\](Ideal gas equation)
Number of molecules …
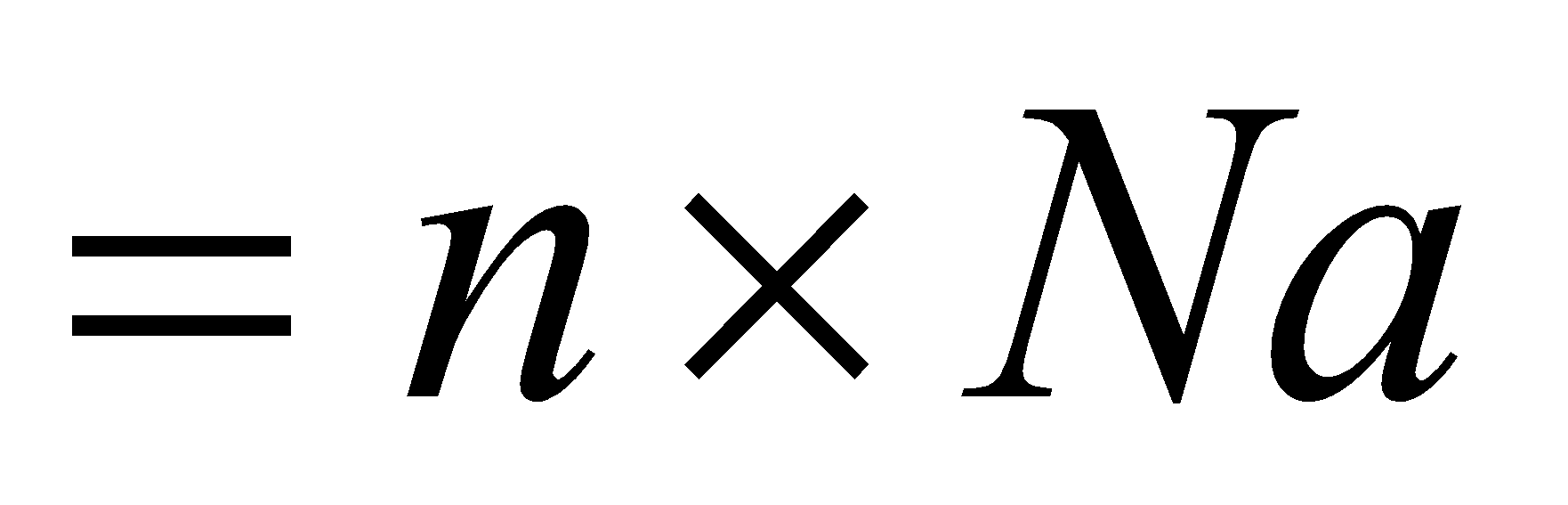 …where Na is Avogadro number
…where Na is Avogadro number
Complete step by step solution:
Let’s look at the answer
The formula for the ideal gas equation is:
\[PV=nRT\]…..Where P is pressure, V is volume, R is gas constant, n is number of moles, and T is absolute temperature.
On transforming the equation for the number of moles, n, we get
\[n=\dfrac{PV}{RT}\]……..eq1
Now, it is given in the question that
\[P={{10}^{-6}}\]of Hg \[=\dfrac{{{10}^{-6}}}{760}atm\]
\[V=1L\]
\[R=0.0821{}^{Latm}/{}_{molK}\]
\[T={{25}^{o}}C=25+273=298K\]
Now, put the values of P, V, T in eq1
We get,
\[n=\dfrac{{{10}^{-6}}\times 1}{760\times 0.0821\times 298}\]……..eq2
Now, using the formula for number of molecules
We get,
Number of molecules ……where Na is Avogadro number
On putting the values of n from eq2 and Na\[=6.02\times {{10}^{23}}\]
We get the number of molecules as:
Number of molecules \[=\dfrac{{{10}^{-6}}\times 6.02\times {{10}^{23}}}{760\times 0.0821\times 298}\]\[=3.2\times {{10}^{13}}\]
So, the number of molecules of the given gas are\[=3.2\times {{10}^{13}}\]
Hence, our final answer is option (B).
Note: The temperature should be converted into kelvin. The pressure should be taken into atmospheres. The value of R should be taken according to the units of P and V. If temperature is not given then take 298K as the standard temperature.
\[PV=nRT\](Ideal gas equation)
Number of molecules …
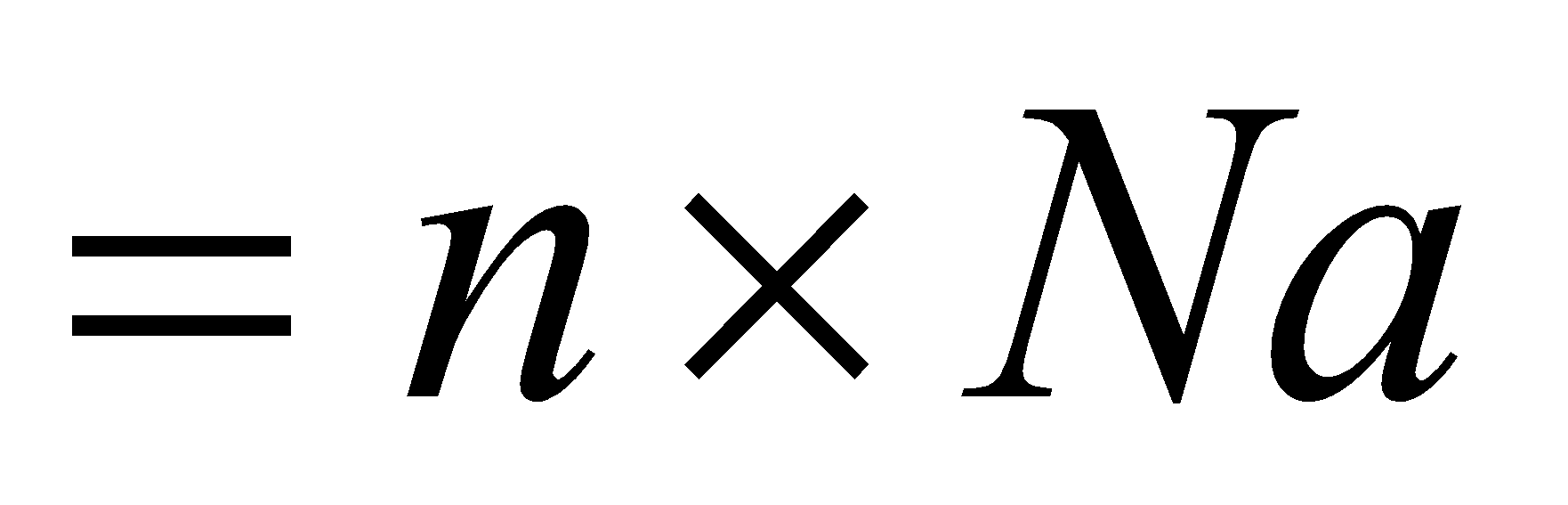
Complete step by step solution:
Let’s look at the answer
The formula for the ideal gas equation is:
\[PV=nRT\]…..Where P is pressure, V is volume, R is gas constant, n is number of moles, and T is absolute temperature.
On transforming the equation for the number of moles, n, we get
\[n=\dfrac{PV}{RT}\]……..eq1
Now, it is given in the question that
\[P={{10}^{-6}}\]of Hg \[=\dfrac{{{10}^{-6}}}{760}atm\]
\[V=1L\]
\[R=0.0821{}^{Latm}/{}_{molK}\]
\[T={{25}^{o}}C=25+273=298K\]
Now, put the values of P, V, T in eq1
We get,
\[n=\dfrac{{{10}^{-6}}\times 1}{760\times 0.0821\times 298}\]……..eq2
Now, using the formula for number of molecules
We get,
Number of molecules ……where Na is Avogadro number
On putting the values of n from eq2 and Na\[=6.02\times {{10}^{23}}\]
We get the number of molecules as:
Number of molecules \[=\dfrac{{{10}^{-6}}\times 6.02\times {{10}^{23}}}{760\times 0.0821\times 298}\]\[=3.2\times {{10}^{13}}\]
So, the number of molecules of the given gas are\[=3.2\times {{10}^{13}}\]
Hence, our final answer is option (B).
Note: The temperature should be converted into kelvin. The pressure should be taken into atmospheres. The value of R should be taken according to the units of P and V. If temperature is not given then take 298K as the standard temperature.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




