Question

1.Draw a rough sketch of two triangles such that they have five pairs of congruent but still triangles are not congruent.
2. If \[\Delta ABC\] and \[\Delta PQR\] are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

Answer 1

Hint: Here we have two problems to be solved. We can first take the problem.1, where we have to sketch two triangles such that they have five pairs of congruent but still triangles are not congruent. We can draw the triangles and explain the congruency for it. For problem.2, we can write one additional pair of corresponding parts using the criterion ASA congruence.

Complete step by step answer:
1.Here we have to draw two triangles such that they have five pairs of congruent but still triangles are not congruent.
We can now draw the diagram of two triangles.

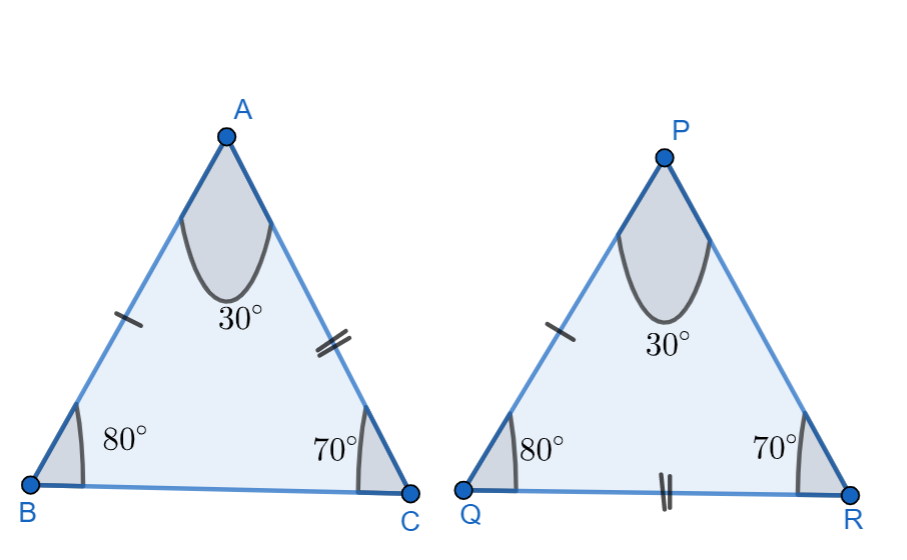
Here we can see that from the diagram,
\[\begin{align}
  & \Rightarrow \angle B=\angle Q={{80}^{\circ }} \\
 & \Rightarrow \angle C=\angle R={{70}^{\circ }} \\
 & \Rightarrow \angle A=\angle P={{30}^{\circ }} \\
 & \Rightarrow AB=PQ \\
 & \Rightarrow AC=QR \\
\end{align}\]
Here we can see that, the five parts of the triangle which are equal,
But here we also have remaining sides BC and PR which are not equal,
\[\Rightarrow BC\ne PR\]
Though 5 parts of the triangle are equal, they are not congruent.
2. If \[\Delta ABC\] and \[\Delta PQR\] are to be congruent, we can name one additional pair of corresponding parts.

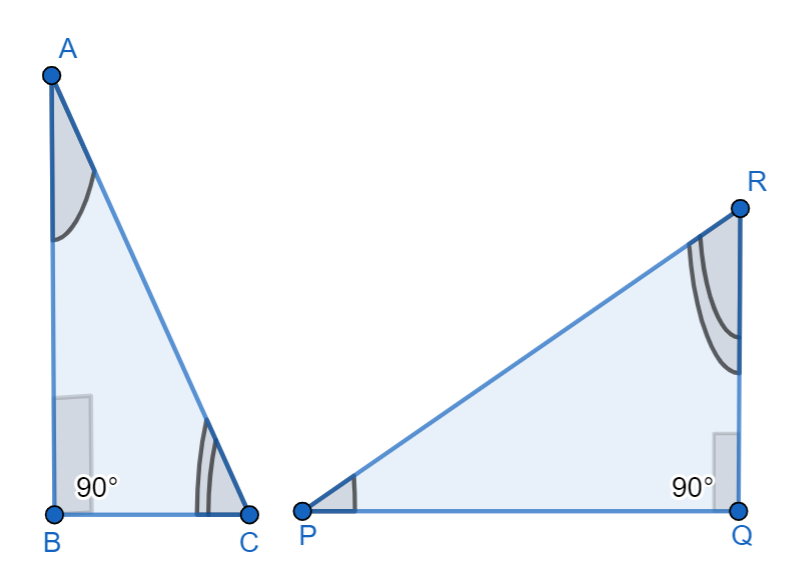
In this given diagram, \[\Delta ABC\] and \[\Delta PQR\] has,
\[\begin{align}
  & \Rightarrow \angle B=\angle Q={{90}^{\circ }} \\
 & \Rightarrow \angle C=\angle R \\
 & \Rightarrow BC=QR \\
\end{align}\] (Given)
Therefore, the\[\Delta ABC\cong \Delta PQR\] has ASA congruence.

Note: We should always remember the congruence rules and concepts to solve these types of problems. We should also remember that, even if we have five parts of a triangle equal, we may also get non congruence for the triangle which we have drawn in this problem.