Question

100 rod is moving on a horizontal surface at an instant when it is parallel to the x-axis its ends A and B have velocities \[20\dfrac{cm}{s}\] and \[30\dfrac{cm}{s}\]
A. Find \[v\] and \[\omega \] of rod.
B. Locate its ICOR.

Answer 1

Hint: Using the formula of angular velocity. Now, taking values given in the figure like: radius, velocity, etc applying on the formula. Calculate further to get the answer of option A. Now, option B using the theory of instantaneous center of rotation and locating the ICOR in the figure.

Complete step-by-step answer:
Part A:
Given that,
Rod radius \[=100cm\]
Velocity of A \[=20\dfrac{cm}{s}\]
Velocity of B \[=30\dfrac{cm}{s}\]

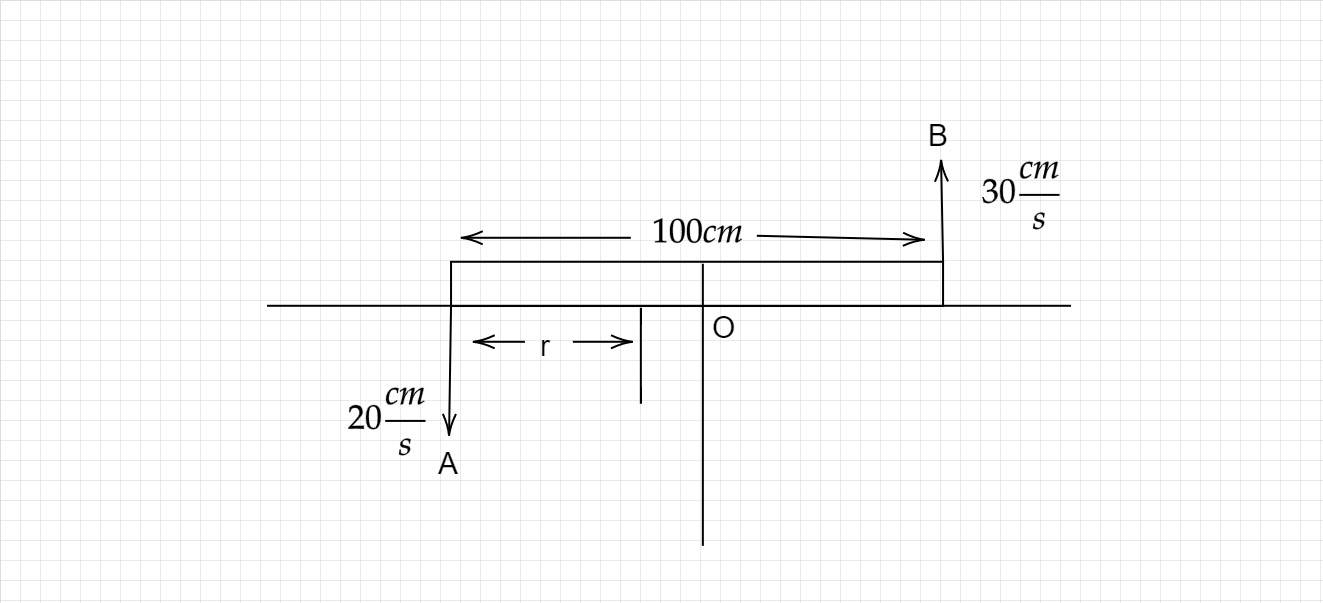
According to the figure:
In mathematically,
\[\omega =\dfrac{v}{r}\]
Let the rod is rotating with uniform angular velocity and the center of rotation of the \[100cm\] rod is \[r\]\[cm\] away from the end rotating with a tangential velocity of\[20\dfrac{cm}{s}\].
Where,\[v=\] linear velocity
\[r=\]Radius
We need to calculate the radius
Using the formula of angular velocity
For A,
\[v=r\omega \]
\[20=r\omega \] .... (I)
For B,
\[30=(100-r)\omega \] ...... (II)
From equation (I) and (II)
\[\dfrac{20}{30}=\dfrac{r}{100-r}\]
\[2000-20r=30r\]
\[r=\dfrac{2000}{50}\]
\[r=40cm\]
We need to calculate the angular velocity
Put the value of r in equation (I)
\[20=40\omega \]
\[\omega =\dfrac{20}{40}\]
\[\omega =0.5rad/s\]
Hence, the angular velocity of the rod is \[0.5rad/s\]
In linear velocity, we can find using equation (1)
\[v=r\omega \]
\[v=0.5rad/s\times 40cm\]
\[v=0.5\times 40\]
\[=20\]
Thus, the linear velocity is \[20cm/s\]
In Part B
The ICOR (instantaneous center of rotation), the point fixed to a body that experience planar movement and that has zero velocity at a particular instantaneous time. At this instant, the velocity vectors of the other points in the body produce a circular field around ICOR which is identical to what is produced by a pure rotation.
If we assume that the rod is rolling then the lowermost point produces a circular field. So if we see the motion from that point at that time then the rod will have a pure rotational motion about that point.

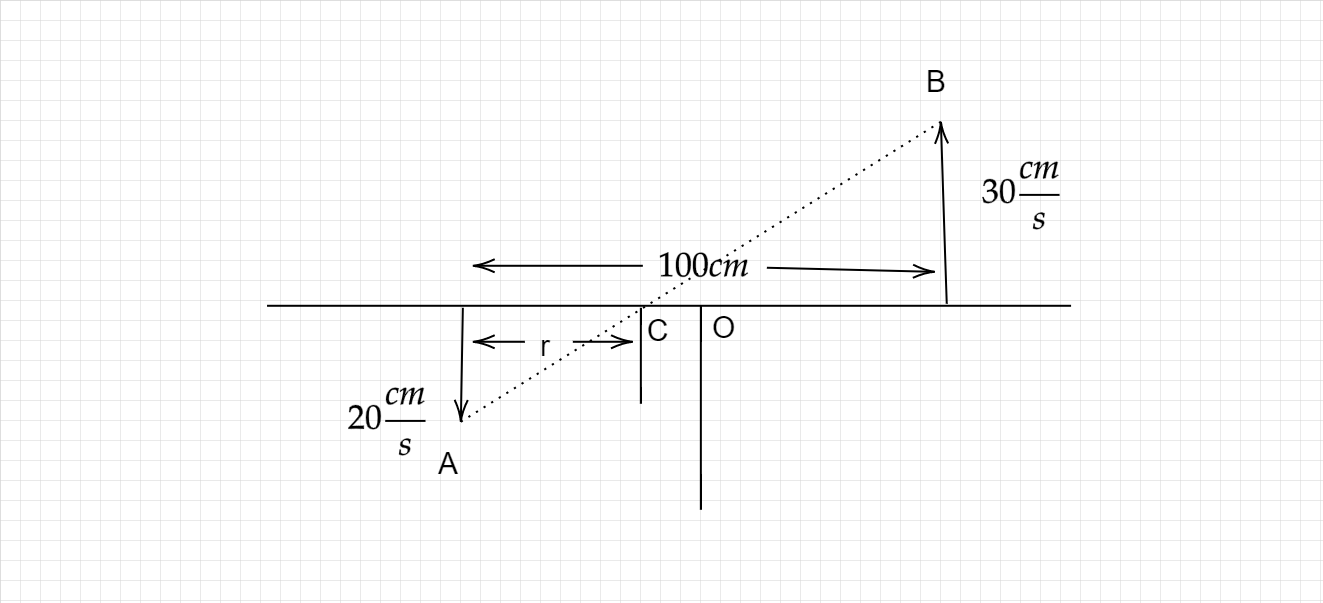
Let’s take the rod when the two parallel velocities are given
Draw two perpendicular lines from the end points of the velocity vectors, where the both the vectors are parallel then line will be drawn as rod position. Now draw a line that joins their heads and that intersects the perpendicular line. That point of intersection is the ICOR.
The point where intersection occurs is at C. Thus, the ICOR of the figure is at C.

Note: Angular velocity is a vector quantity and is described as the rate of change of angular displacement. The amount of change of angular displacement of the particle at a given period of time is called angular velocity. The track of the angular velocity vector is vertical to the plane of rotation, in a direction which is usually indicated by the right-hand rule.