
1) Write molecularity of the following reaction:
$2NO(g) + {O_2}(g) \to 2N{O_2}(g)$
2) What is 'calcination'? How does it differ from 'roasting'?
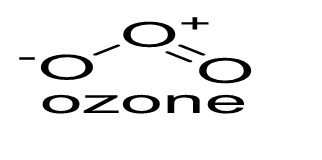
3) Write resonating structures of ozones,
4) The decomposition of N2O5(g) at 320 K according to the following equation follows first order reaction:
${N_2}{O_5}(g) \to 2N{O_2}(g) + 21{O_2}(g)$
The initial concentration of ${N_2}{O_5}$(g) is $1.24\times 10^{−2}mol.L^{−1}$ and after 60 minutes, $0.20\times 10^{−2}mol.^L{−1}$. Calculate the rate constant of the reaction at 320 K
Answer
578.7k+ views
Hint: The order of reaction can be defined as an empirical quantity which is estimated through experiment via the rate law of reaction. It is actually the sum of the exponent equation of the rate laws. On the other hand, molecularity is usually deduced from elementary reaction mechanisms and is utilised only in reference of an elementary reaction.
Complete step by step answer:
1) Molecularity refers to the summation of different reactants participating in a balanced equation of a chemical reaction. Now calculate the molecularity of the given reaction:
$2NO(g) + {O_2}(g) \to 2N{O_2}(g)$
In this chemical reaction, 2 molecules of NO react with 1 molecule of $O_2$. Thus, the total number of reactants in this balanced equation of chemical reaction = 2 + 1 = 3.
As a result, the molecularity of the given reaction is 3.
2) Calcination: Calcination is a thermal decomposition process in which ore is heated below their melting point in the absence of air in order to detach volatile impurities.
Example: Thermal decomposition of Zinc carbonate minerals to drive off $CO_2$.
\[ZnC{O_3}\left( s \right) \to ZnO\left( s \right) + C{O_2}\left( g \right)\]
The difference between Calcination and Roasting is indicated in the following table:
3) Ozone ($O_3$) comprises two resonating structures (I and II). The structure of ozone and its resonating structures are given below:
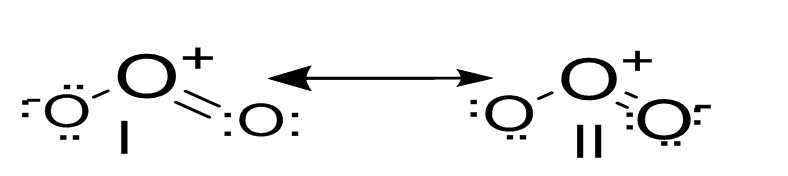
Each atom is roughly $sp^2$ hybrid. The O atom in the centre consists of a lone pair of electrons having a delocalised π orbital over other three oxygen atoms.
4) The rate constant (K) for the first order reaction at a temperature, t can be stated as below:
$K = \dfrac{{2.303}}{t}\log \dfrac{{{C_0}}}{{{C_t}}}$
Here, $C_o$ refers to the initial concentration and $C_t$ refers to the concentration after a time, t
For the given reaction:
${N_2}{O_5}(g) \to 2N{O_2}(g) + 21{O_2}(g)$
Given values are: $C_o=1.24\times 10^{−2}mol.L^{−1}$,$C_t=0.20\times 10^{−2}mol.^L{−1}$,t=60 min
Now, find the value of K by putting the given values in the formula
$
K = \dfrac{{2.303}}{{60}}\log \dfrac{{1.24 \times {{10}^{ - 2}}mol{L^{ - 1}}}}{{0.20 \times {{10}^{ - 2}}mol{L^{ - 1}}}}
= 0.038 \times 0.792{\min ^{ - 1}} = 0.030{\min ^{ - 1}}
$
As a result, the rate constant of the reaction at 320K is $0.030 min^{−1}.$
Note:
A resonance form of structure is another method to draw a Lewis dot structure of a specific compound. Equivalent forms of Lewis structures are known as resonance structures. These resonance forms are employed when more than one method is available to position double bonds as well as lone pairs over atoms. We draw the resonance forms when one structure is not capable of showing its real structure.
Complete step by step answer:
1) Molecularity refers to the summation of different reactants participating in a balanced equation of a chemical reaction. Now calculate the molecularity of the given reaction:
$2NO(g) + {O_2}(g) \to 2N{O_2}(g)$
In this chemical reaction, 2 molecules of NO react with 1 molecule of $O_2$. Thus, the total number of reactants in this balanced equation of chemical reaction = 2 + 1 = 3.
As a result, the molecularity of the given reaction is 3.
2) Calcination: Calcination is a thermal decomposition process in which ore is heated below their melting point in the absence of air in order to detach volatile impurities.
Example: Thermal decomposition of Zinc carbonate minerals to drive off $CO_2$.
\[ZnC{O_3}\left( s \right) \to ZnO\left( s \right) + C{O_2}\left( g \right)\]
The difference between Calcination and Roasting is indicated in the following table:
| S.No. | Calcination | Roasting |
| i | Thermal decomposition takes place in the absence of air | Thermal decomposition takes place in the presence of air |
| ii | This process is applied for carbonate ores. | This method is applied for sulphide ores. |
| iii | Carbon dioxide ($CO_2$) is yielded with metal oxide. | Sulphur dioxide ($SO_2$) is yielded with metal oxide. |
| iv | Examples:\[ZnC{O_3}\left( s \right) \to ZnO\left( s \right) + C{O_2}\left( g \right)\]\[CuC{O_3}\left( s \right) \to CuO\left( s \right) + C{O_2}\left( g \right)\] | Examples:\[2ZnS\left( s \right) + 3{O_2} \to 2ZnO\left( s \right) + 2S{O_2}\left( g \right)\]\[2C{u_2}S\left( s \right) + 3{O_2} \to 2C{u_2}O\left( s \right) + 2S{O_2}\left( g \right)\] |
3) Ozone ($O_3$) comprises two resonating structures (I and II). The structure of ozone and its resonating structures are given below:


Each atom is roughly $sp^2$ hybrid. The O atom in the centre consists of a lone pair of electrons having a delocalised π orbital over other three oxygen atoms.
4) The rate constant (K) for the first order reaction at a temperature, t can be stated as below:
$K = \dfrac{{2.303}}{t}\log \dfrac{{{C_0}}}{{{C_t}}}$
Here, $C_o$ refers to the initial concentration and $C_t$ refers to the concentration after a time, t
For the given reaction:
${N_2}{O_5}(g) \to 2N{O_2}(g) + 21{O_2}(g)$
Given values are: $C_o=1.24\times 10^{−2}mol.L^{−1}$,$C_t=0.20\times 10^{−2}mol.^L{−1}$,t=60 min
Now, find the value of K by putting the given values in the formula
$
K = \dfrac{{2.303}}{{60}}\log \dfrac{{1.24 \times {{10}^{ - 2}}mol{L^{ - 1}}}}{{0.20 \times {{10}^{ - 2}}mol{L^{ - 1}}}}
= 0.038 \times 0.792{\min ^{ - 1}} = 0.030{\min ^{ - 1}}
$
As a result, the rate constant of the reaction at 320K is $0.030 min^{−1}.$
Note:
A resonance form of structure is another method to draw a Lewis dot structure of a specific compound. Equivalent forms of Lewis structures are known as resonance structures. These resonance forms are employed when more than one method is available to position double bonds as well as lone pairs over atoms. We draw the resonance forms when one structure is not capable of showing its real structure.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE




