Question

1) The wheels of a car are of diameter 80cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66km per hour?
2) Tick the correct answer in the following and justify your choice, if the perimeter and the area of a circle are numerically equal, then the radius of the circle is:
\[\begin{align}
  & \text{A}.\text{ 2 units} \\
 & \text{B}.\text{ }\pi \text{ units} \\
 & \text{C}.\text{ 4 units} \\
 & \text{D}.\text{ 7 units} \\
\end{align}\]

Answer 1

Hint: For the first part, the question is somewhat based on a circular rotation concept. The approach is simple. We have a linear speed given. Now, we have to find the angular speed, for that, we apply v=wr where, w = angular speed and r = radius of the wheel. Once we find the angular speed then convert the angular speed into revolution per minute (rpm) using formula \[\left[ 1\text{ rad/sec}=\dfrac{1}{2\pi }\text{ revolution per sec} \right]\]
For the second part, the question uses a very elementary formula regarding circles. We have to just follow what the given condition is and solve it accordingly. We all know that formula for the perimeter of the circle would be: $P=2\pi r$ and the area of the circle is $A={{\pi }^{2}}$ where r = radius of the circle.

Complete step by step answer:
1) Now, moving to the question, we have given data as v=66 kmph, where v = linear speed.
Now, we will convert this speed to SI unit (i.e. m/s) using the below conversion,
\[1kmph=\dfrac{1000}{60\times 60}\dfrac{m}{\sec }=\dfrac{5}{18}m/s\]
Hence, we get the value of v as
\[\begin{align}
  & 66kmph=66\times \dfrac{5}{18}m/s \\
 & \Rightarrow \left( \dfrac{55}{3} \right)m/s \\
 & \therefore v=\left( \dfrac{55}{3} \right)m/s \\
\end{align}\]
Now, we will consider a circle as shown below,

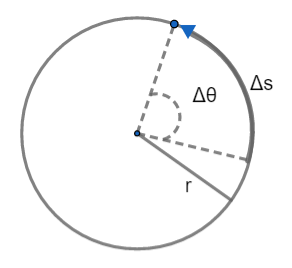
$\Delta S$ is the arc length along the circle $\Delta S=r\Delta \theta $
Linear speed along circle: \[v=\dfrac{ds}{dt}\Rightarrow v=\dfrac{rd\theta }{dt}\]
Therefore, angular speed: \[\begin{align}
  & w=\dfrac{d\theta }{dt}=\dfrac{v}{r} \\
 & \therefore v=rw \\
\end{align}\]
Hence, we have $w=\dfrac{v}{r}$
Where, \[v=\dfrac{55}{3}m/s,r=\dfrac{80cm}{2}=40cm=0.4m\left( \because \text{Diameter}=80cm \right)\]
\[\therefore w=\dfrac{\dfrac{55}{3}}{0.4}=\dfrac{55\times 10}{3\times 4}=\dfrac{275}{6}\text{ radian/sec}\]
Now, we know,
\[\begin{align}
  & 1\text{ rad/sec}=\dfrac{1}{2\pi }\text{ revolution per sec}\left( rps \right) \\
 & 1\text{ rad/sec}=\dfrac{60}{2\pi }\text{ revolution per minute}\left( rpm \right) \\
\end{align}\]
Therefore, in
\[\dfrac{275}{6}\text{ rad/sec}=\dfrac{60}{2\pi }\times \dfrac{275}{6}\left( rpm \right)=\left( \dfrac{5\times 275}{\pi } \right)rpm\]
Hence, we have,
In one minute \[\to \left( \dfrac{5\times 275}{\pi } \right)\text{ revolutions}\]
Therefore, we have
\[\text{In ten minutes}\to \left( \dfrac{5\times 275}{\pi }\times 10 \right)\text{revolutions}\]
Hence, we get
\[\begin{align}
  & \Rightarrow \dfrac{5\times 275\times 10}{\pi } \\
 & \Rightarrow \tilde{=}4378.98\left( \text{Take }\pi =3.14 \right) \\
\end{align}\]

2) We have been given information as, "Perimeter and area of a circle are numerically equal". Hence, we get
 \[\begin{align}
  & P=A \\
 & \Rightarrow 2\pi r=\pi {{r}^{2}} \\
 & \Rightarrow \pi {{r}^{2}}-2\pi r=0 \\
 & \Rightarrow \pi r\left( r-2 \right)=0\left( \text{taking }\pi r\text{ as common} \right) \\
\end{align}\]
Now, we know that $\pi r\ne 0$ because $\pi =3.14$ and r = radius of circle (which can't be zero).
Hence, we can write that
\[\begin{align}
  & \Rightarrow \pi r\left( r-2 \right)=0 \\
 & \Rightarrow \pi r\ne 0 \\
 & \therefore r-2=0 \\
 & \Rightarrow r=2\text{ units} \\
\end{align}\]
Therefore, the radius of the circle will be 2 units.

Note: In the question, we have taken a value of $\pi =3.14$. If we want to express it in fraction form then take it as $\pi =\left( \dfrac{22}{7} \right)$ . There are a lot of conversions being used in the solution, so care must be taken not to mess up any of them.
For the second part, simple concepts are applied in the question. Very few chances of getting errors. There is a point in the question, where we have converted rps to rpm. Sometimes here, students take rpm as rps which is wrong, they should convert rps by multiplying it with 60 properly.