Question

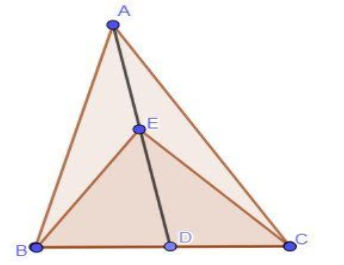
1) In fig. 9.23, \[E\] is any point on the median \[AD\] of a \[\Delta ABC\]. Show that \[ar\left( {ABE} \right) = ar\left( {ACE} \right)\].
2) In a triangle \[ABC\], \[E\] is the midpoint of median \[AD\]. Show that \[ar\left( {BED} \right) = \dfrac{1}{4}ar\left( {ABC} \right)\].

Answer 1

Hint:
1) Since \[AD\] is the median of \[\Delta ABC\] and \[ED\]is the median of \[\Delta EBC\], we will use the property that the median divides a triangle into 2 triangles of equal area. Then we will subtract the 2 equations that we get to obtain the required results.
2) As \[E\] is the midpoint of \[AD\], \[BE\] will be the median of \[\Delta ABD\]. Since \[AD\] is the median of \[\Delta ABC\] and \[BE\] is the median of \[\Delta ABD\], we will use the property that the median divides a triangle into 2 triangles of equal area. We will use the 2 equations that we get to obtain the required results.

Complete step by step solution:
1) In \[\Delta ABC\], \[AD\]is the median. \[D\] is the midpoint of \[BC\]. The median of a triangle divides the triangle into 2 triangles of equal area. Let’s represent this in the form of an equation.
\[ar\left( {ABD} \right) = ar\left( {ACD} \right){\text{ }}\left( 1 \right)\]
As \[D\] is the midpoint of \[BC\], \[ED\] is the median of \[\Delta EBC\]. The median of a triangle divides the triangle into 2 triangles of equal area. Let’s represent this in the form of an equation.
\[ar\left( {EBD} \right) = ar\left( {ECD} \right){\text{ }}\left( 2 \right)\]
Let’s subtract equation (2) from equation (1).
\[\begin{array}{l}ar\left( {ABD} \right) - ar\left( {EBD} \right) = ar\left( {ACD} \right) - ar\left( {ECD} \right)\\ \Rightarrow ar\left( {ABE} \right) = ar\left( {ACE} \right)\end{array}\]
Hence, proved that \[ar\left( {ABE} \right) = ar\left( {ACE} \right)\].
2. In \[\Delta ABC\], \[AD\]is the median. \[D\] is the midpoint of \[BC\]. The median of a triangle divides the triangle into 2 triangles of equal area. Let’s represent this in the form of an equation.
\[ar\left( {ABD} \right) = ar\left( {ACD} \right)\]
We can see from the figure that
\[\begin{array}{l}ar\left( {ABD} \right) + ar\left( {ACD} \right) = ar\left( {ABC} \right)\\ \Rightarrow ar\left( {ABD} \right) + ar\left( {ABD} \right) = ar\left( {ABC} \right)\\ \Rightarrow 2ar\left( {ABD} \right) = ar\left( {ABC} \right)\\ \Rightarrow ar\left( {ABD} \right) = \dfrac{1}{2}ar\left( {ABC} \right){\text{ }}\left( 1 \right)\end{array}\]
As \[E\] is the midpoint of \[AD\], \[BE\] will be the median of \[\Delta ABD\].
In \[\Delta ABD\], \[BE\] is the median. The median of a triangle divides the triangle into 2 triangles of equal area. Let’s represent this in the form of an equation.
\[ar\left( {BED} \right) = ar\left( {BEA} \right)\]
We can see from the figure that
\[\begin{array}{l}ar\left( {BED} \right) + ar\left( {BEA} \right) = ar\left( {ABD} \right)\\ \Rightarrow ar\left( {BED} \right) + ar\left( {BED} \right) = ar\left( {ABD} \right)\\ \Rightarrow 2ar\left( {BED} \right) = ar\left( {ABD} \right)\\ \Rightarrow ar\left( {BED} \right) = \dfrac{1}{2}ar\left( {ABD} \right){\text{ }}\left( 2 \right)\end{array}\]
Substitute equation (1) in equation (2):
\[\begin{array}{l}ar\left( {BED} \right) = \dfrac{1}{2}\left( {\dfrac{1}{2}ar\left( {ABC} \right)} \right)\\ \Rightarrow ar\left( {BED} \right) = \dfrac{1}{4}ar\left( {ABC} \right)\end{array}\]

Hence, proved that \[ar\left( {BED} \right) = \dfrac{1}{4}ar\left( {ABC} \right)\].

Note:
\[BE\] is the median of \[\Delta ABD\] because any line connecting the vertex of a triangle to the midpoint of the opposite side is considered to be the median of that triangle.