NCERT Solutions For Class 8 Maths Chapter 11 Mensuration in Hindi - 2025-26
FAQs on NCERT Solutions For Class 8 Maths In Hindi Chapter 11 Mensuration - 2025-26
1. Where can I find reliable, step-by-step NCERT Solutions for Class 8 Maths Chapter 11, Mensuration?
You can find comprehensive and accurate NCERT Solutions for Class 8 Maths Chapter 11 (Mensuration) on Vedantu. These solutions are prepared by subject matter experts and follow the latest CBSE 2025-26 guidelines. Each solution provides a detailed, step-by-step method to solve the problems, ensuring conceptual clarity and helping you score better in exams.
2. Is it necessary to solve every question from the NCERT textbook for Class 8 Maths Mensuration?
Yes, it is highly recommended to solve every single question from the NCERT textbook for Mensuration. Practising all the problems, including the examples and exercise questions, ensures you have a strong command of all the concepts and formulas. The NCERT Solutions provide the correct methodology for each problem, which is crucial for mastering the chapter.
3. How are the NCERT Solutions for Class 8 Maths Mensuration structured to help with exam preparation?
The NCERT Solutions for Class 8 Maths Mensuration are structured exercise-wise for easy navigation. Each solution offers:
- A clear, step-by-step approach to reach the final answer.
- The specific formulas used for solving the problem.
- Detailed explanations to clarify complex concepts like surface area and volume.
- Adherence to the CBSE-prescribed format for writing answers in exams.
4. What is the correct method to use these NCERT Solutions for effective practice?
For the most effective practice, first, try to solve the NCERT textbook questions on your own. If you get stuck or want to verify your answer, refer to the step-by-step NCERT Solutions. This method helps you identify your weak areas, understand the correct problem-solving approach, and build confidence. Do not just copy the solutions; use them as a guide to learn the methodology.
5. Why is the Mensuration chapter sometimes listed as Chapter 9 and sometimes as Chapter 11 for Class 8 Maths?
This is due to the syllabus rationalisation by NCERT. In the older NCERT textbook, Mensuration was Chapter 11. In the new, rationalised textbook used for the 2025-26 academic session, Mensuration is Chapter 9. Our NCERT Solutions cover the complete Mensuration syllabus as per the current curriculum, and the solutions provided here are for all the exercises in this chapter.
6. How do the NCERT Solutions help in understanding the real-world application of mensuration formulas?
The NCERT textbook for Class 8 Mensuration includes many problems based on real-world scenarios, such as finding the area of a field, the volume of a water tank, or the cost of painting a wall. The NCERT Solutions break down these word problems into simple steps, showing you exactly how to apply formulas like the area of a trapezium or the volume of a cylinder to practical situations.
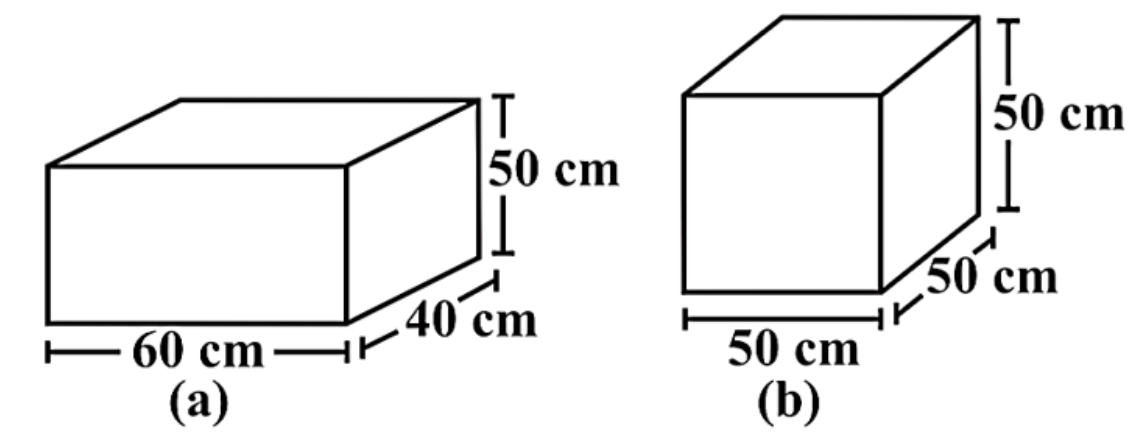
7. How do the solutions explain calculating the surface area of a cube versus a cuboid?
The NCERT Solutions clearly distinguish between these two calculations. For a cube, where all sides (l) are equal, the solution demonstrates using the formula 6l². For a cuboid, with different length (l), breadth (b), and height (h), the solutions guide you through the step-by-step application of the formula 2(lb + bh + hl), ensuring you don't confuse the two concepts.
8. What approach is taught in the NCERT Solutions for problems involving combined shapes?
For complex problems involving combined shapes (e.g., a building with a cylindrical part and a conical top), the NCERT Solutions teach a systematic approach. The method involves:
- Breaking the complex figure down into its basic geometric shapes (e.g., cylinder, cone).
- Calculating the required parameter (like area or volume) for each individual shape.
- Adding or subtracting these values as required by the problem to find the final answer.