Triangle Congruence Theorem

Triangle Congruence Theorem is a fundamental tool of Geometry and two figures in geometry are said to be congruent if they are of exactly the same size and shape. We use Triangle Congruence Theorems to prove if the triangles are congruent or not. In this article, we will discuss the methods to prove triangles congruent in detail.

Statement of Triangle Congruence Theorem

Triangle Congruence Theorem is as follows:

• Angle Side Angle Congruence Theorem: Two triangles are congruent if the two corresponding angles equal to each other include a corresponding side that is equal to each other in two triangles.

• Side Angle Side Congruence Theorem: Two triangles are congruent if two sides of two triangles are equal including the corresponding angles formed by these sides also equal.

• Side Side Side Congruence Theorem: According to SSS congruence theorem, the two triangles are said to be congruent, if three sides of a triangle are equal to the corresponding sides of the other triangle.

Proof of Triangle Congruence Theorem

Angle Side Angle Congruence Theorem

Two triangles are congruent if the two corresponding angles equal to each other include a corresponding side that is equal to each other in two triangles.

Proof:

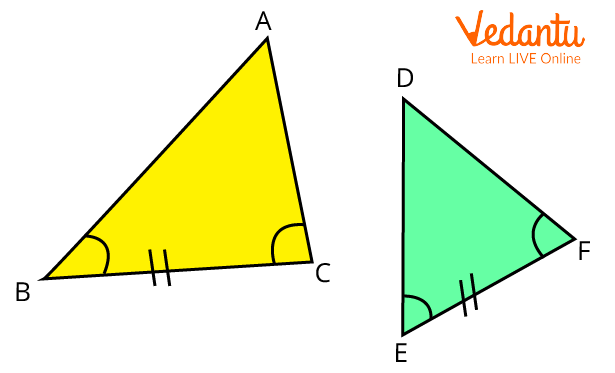
Triangles ABC and DEF for ASA Theorem

Given:

$B C=E F$

$\angle B=\angle E$

$\angle C=\angle F$

Superimposing both the triangles and aligning them according to the angles and sides.

Align side $E F$ with side $B C$.

Also, $\angle B=\angle E$.

So, the direction of side $E D$ will be the same as the direction of side $B A$.

Also, $\angle C=\angle F$

So, the direction of side $F D$ will be the same as the direction of side $C A$.

So, we can say that the point of intersection of sides $E D$ and $F D$ (that is $D$ ) will coincide exactly with the point of intersection of sides $B A$ and $C A$ (that is $A$ ).

Hence, we can say that both triangles are same in shape and size,

So,

$\triangle A B C \cong \triangle D E F$

Side Angle Side Congruence Theorem

Two triangles are congruent if two sides of two triangles are equal including the corresponding angles formed by these sides also equal.

Proof:

Given: $A B=P Q, B C=Q R, \angle B=\angle Q$.

To prove: $\triangle A B C \cong \triangle P Q R$

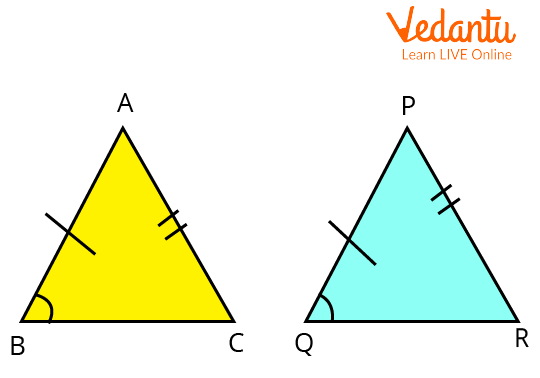
Triangles ABC and PQR for SAS Theorem

As done in $A S A$, again superimpose triangles here.

Place the triangle $\triangle A B C$ over the triangle $\triangle P Q R$ in a way that angle $B$ falls on angle $Q$ and side $A B$ falls on the side $P Q$. It is given that $A B=P Q$, so point $A$ falls on point $P$, and $\angle B=\angle Q$, so the side $B C$ will fall on the side $Q R$, and $B C=Q R$, so point $C$ will fall on point $R$.

Therefore, side $B C$ coincides with side $Q R$ and side $A C$ coincides with side $P R$.

So, we have $\triangle A B C \cong \triangle P Q R$.

Hence Proved.

Side Side Side Congruence Theorem

According to the $SSS$ congruence theorem, the two triangles are said to be congruent, if three sides of a triangle are equal to the corresponding sides of the other triangle. Proof:

Given: All sides are equal, i.e., $A B=D E, A C=D F, B C=E F$.

To prove: $\triangle A B C \cong \triangle D E F$.

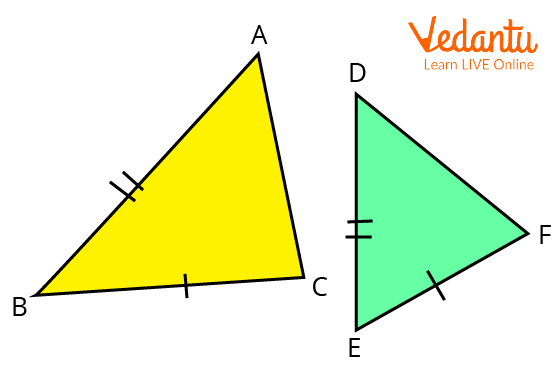
Triangles ABC and DEF for SSS Theorem

All three sides of both triangles are of the same size and length.

On superimposing both the triangles,

Side $D E$ will be on the side $A B$,

Side $E F$ will be on the side $B C$, and

side $D F$ will be on the side $A C$.

Therefore, $\triangle A B C \cong \triangle D E F$.

Hence proved.

Limitations of Triangle Congruence Theorem

• Triangle Congruence theorems are applicable only if triangles are the same in both shape and size.

Applications of Triangle Congruence Theorem

Triangle Congruence Theorem has a wide range of applications in our day-to-day life.

• A Truss bridge is made using equilateral triangles applying the triangle congruence theorem.

• The theorem is used in understanding the structure of the environment.

Solved Examples

1. Describe the type of congruence in two triangles given by

$\triangle A B C, A B=7 \mathrm{~cm}, B C=5 \mathrm{~cm}, \angle B=50^{\circ}$ and $\triangle D E F, D E=5 \mathrm{~cm}, E F=7 \mathrm{~cm}, \angle E$ $=50^{\circ}$.

Ans:
$A B=E F=7 \mathrm{~cm},$

$B C=D E=5 \mathrm{~cm}$ and

$\angle B=\angle E=50^{\circ}$

So from above, we can say that both triangles are congruent using the SAS congruence criteria.

Therefore, $\triangle A B C \cong \triangle F E D$ (SAS).

2. In a $\triangle A B C$, if $A B=A C$ and $\angle B=70^{\circ}$, find $\angle A$.

Ans:

In a $\triangle A B C, A B=A C$ and $\angle B=70^{\circ}$

$\angle B=\angle C$ (as angles opposite to equal sides of a triangle are also equal)

Therefore, $\angle B=\angle C=70^{\circ}$

Sum of angles in a triangle $=180^{\circ}$

$\angle A+\angle B+\angle C=180^{\circ} $

$\angle A+70^{\circ}+70^{\circ}=180^{\circ} $

$\angle A=180^{\circ}-140^{\circ} $

$\angle A=40^{\circ}$

3. In the given congruent triangles under $A S A$, find the value of $x$ and $y$ where $QR=TU$.

Ans:

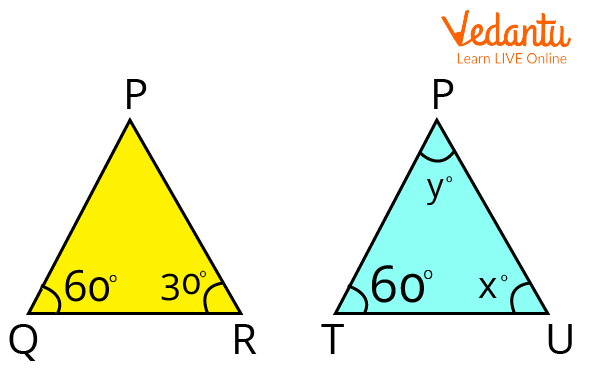
Triangles PQR and PTU given in the question

Given: $\triangle P Q R=\triangle P T U$ (By ASA rule)

$\angle Q=\angle T=60^{\circ}$ (given)

$QR=TU$

$\angle x=30^{\circ}$ (for ASA rule)

Now in $\triangle \mathrm{PTU}$,

$\angle P+\angle T+\angle U=180^{\circ}$ (Angle sum property)

$\angle y+60^{\circ}+\angle x=180^{\circ}$

$\angle y+60^{\circ}+30^{\circ}=180^{\circ}$

$\angle y+90^{\circ}=180^{\circ}$

$\angle y=180^{\circ}-90^{\circ}=90^{\circ}$

Hence, $x=30^{\circ}$ and $y=90^{\circ}$.

Conclusion

In the article, we have discussed the detailed proof of Triangle Congruence Theorems. All the different ways to prove that the triangles are congruent are discussed above. Real-life examples of the theorem are also discussed. The Triangle Congruence theorem forms an important tool of geometry and is an essential element of geometry to study objects of the same size and shape.