Introduction
Because it increases the amount, money division is less enjoyable to think about as money addition or multiplication. After all, most of us would choose to increase our income over dividing it. However, the capacity to divide the money is an important skill for good money management. It helps us calculate things like the cost of an item per ounce or a good.
Division of Money
What is Division?
The basic purpose of the division is to produce equal groups or to verify how many individuals are in each category following a fair distribution.
The four main parts of division are the dividend, the divisor, the quotient, and the remainder. Every day, we use the division approach in various situations.
How Division Works
Let's start by splitting some numbers; it's not that difficult. Remember to fit the decimal points in the dividend, and the quotient is, by far, the most important factor.
When you are dividing to calculate the unit cost of something or anything else that could create a rupee value, remember the rupee symbol first. Second, you don't need to divide money amounts by more than three decimal places because we can't pay in fractions of paisa. Using three decimal places serves the primary task of providing that we know whether to round up or down.
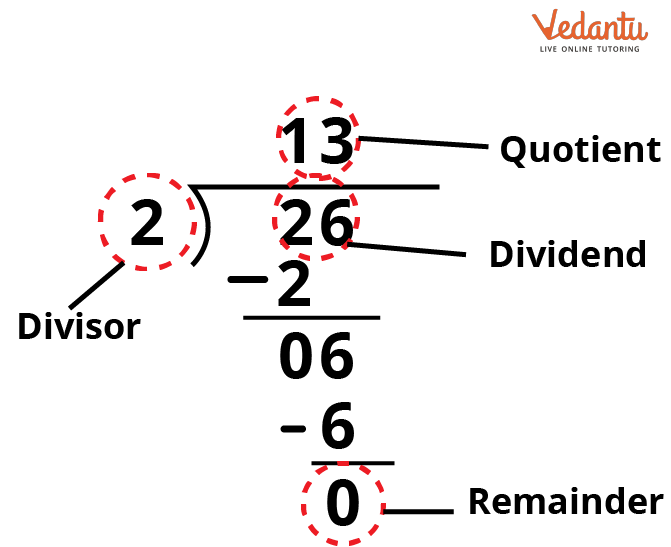
Parts of Division
Money Divider Calculator
Long division is used to divide a given sum of money into an exact number of equal individual units, known as money division.
To divide the money, enter any amount of money and the number you want to divide it into the calculator. Given the other factors, this calculator can also calculate either the initial sum or the total number of divisions.
Money Calculator
The formula used to calculate money division is $MD = \dfrac{D}{X}$.
Where MD has divided the money, D is the original amount, and X is the number to divide with.
Examples of Money Division
Let us look at some money division examples:
Example 1: Find the quotient.
$5\overline{)626.63}$
Solution:
We need to find the quotient when 626.63 is divided by 5.
We will perform the long division,
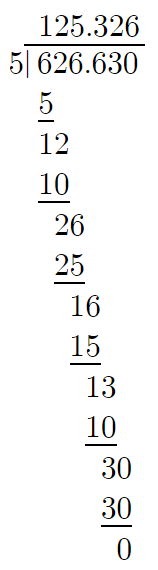
626.63/5
The quotient obtained by dividing 626.63 by 5 is 125.326.
As there cannot be more than 2 digits after the decimal, then we will have to round off the decimal places. On rounding off, we get 125.33.
Therefore, on performing long division on 626.63 by 5, the quotient we get is 125.33.
Example 2: Find the quotient.
$5\overline{)3,295.15}$
Solution:
We need to find the quotient when 3,295.15 is divided by 2.
We will perform the long division,
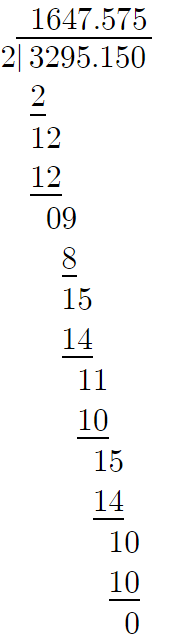
3295.15/2
The quotient obtained by dividing 3,295.15 by 2 is 1,647.575.
As there cannot be more than 2 digits after the decimal, then we will have to round off the decimal places. On rounding off, we get 1,647.58.
Therefore, on performing long division on 3,295.15 by 2, the quotient we get is 1,647.58.
Example 3: Find the quotient:
$7\overline{)2,341.92}$
Solution:
We need to find the quotient when 2,341.92 is divided by 7.
We will perform the long division,
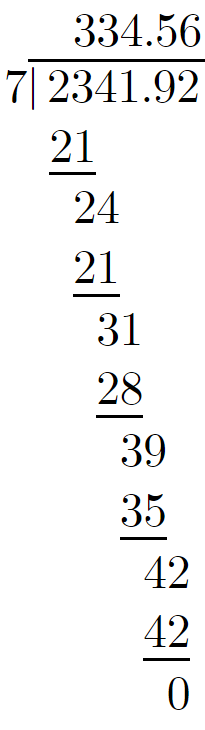
2341.92/7
Therefore, on performing the long division on 2,341.15 by 7, the quotient we get is 334.56.
Dividing Money Worksheets
Do your children realise who gets the money worksheet's free answer key? You people, of course! So, let’s get started:
Q1: Find the quotient:
$6\overline{)21.6}$
Solution:
We need to find the quotient when 21.6 is divided by 6.
We will perform the long division,
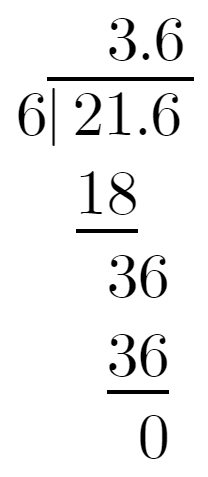
21.6/6
On performing the long division on 21.6 by 6, the quotient is 3.6.
Q2: Find the quotient:
$6\overline{)82.74}$
Solution:
We need to find the quotient when 82.74 is divided by 6.
We will perform the long division,
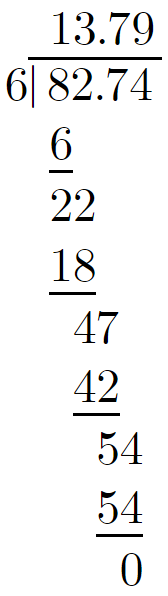
82.74/6
On performing the long division on 82.74 by 6, the quotient is 13.79.
Q3: Sima was asked to distribute ₹942.12 to 9 of her classmates. How much will each one of her classmates receive in terms of money?
Solution:
To divide ₹942.12 among 9 of Sima’s classmates.
We will have to perform the long division,
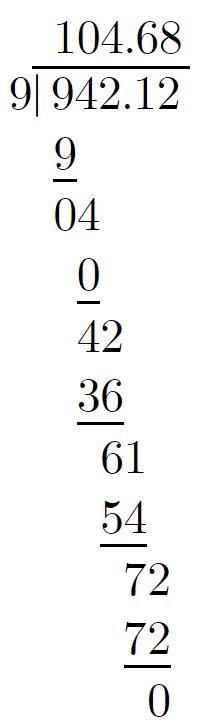
942.12/9
Dividing ₹942.12 among 9 of Sima’s classmates is ₹104.68.
Q4: Simba bought five chocolates for ₹56.25. How much does one chocolate cost?
Solution:
From the given question,
The cost of 5 chocolates is ₹56.25.
To find the cost of 1 chocolate, we will have to perform a long division where ₹56.25 is divided by 5 chocolates.
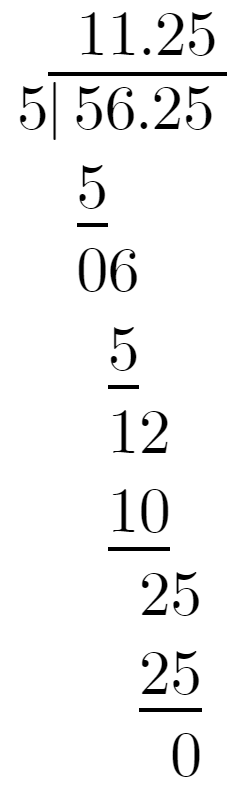
56.25/5
The cost of 1 chocolate that Simba bought is ₹11.25.
Conclusion
In this article, we have learned about the basic arithmetic operation, i.e. division. The division is used to distribute things equally. Division breaks down a large group into smaller parts. Division can also be separated into two parts, areas or groups. Every arithmetic operation has its unique symbol. In division, the sign is ‘÷’ or ‘/’ or ‘_’.
FAQs on Money Division
1. What is the money division used for?
When someone wants to split an amount evenly among a particular number of people, they divide the value.
2. Name one example where money division is used.
One example where money division is used is when we split the bill at the restaurant among the people.
3. What different types of division exist?
A division method is a process used to divide something. According to the difficulty level, there are three different sorts of division procedures. These include the bus stop method, the long division method, and the chunking approach, often known as division by repeated subtraction.
