




Step-by-Step Guide to Finding Factors of 250
The numbers that when multiplied together, result in the number 250 are called factors of 250. For instance, when we multiply 2 and 5, we get 10, which means that 2 and 5 are factors of 10. The factors of the number 250 may be discovered in the same way. You will learn the factors of 250, how to discover the factors of a number 250, and the prime factors of 250 in this article, along with clear instructions.
What are the Factors of 250?
A factor of an integer is another integer that can divide the integer without leaving any remainder. So, the factors of 250 are the numbers that divide 250 exactly without a remainder. Hence, all factors of 250 are 1, 2, 5, 10, 25, 50, 125 and 250.
How Can We Find the Factors for 250?
To calculate the factor of 250, just divide 250 by all the integers from 1 to 250. Also, find the integer that divides 250 without leaving a remainder. Let's do it and figure out all the 250 factors.
1 is a factor of 250.
\[250\div 1=250\]
2 is a factor of 250.
\[250\div 2=125\]
5 is a factor of 250.
\[250\div 5=50\]
10 is a factor of 250.
\[250\div 10=25\]
25 is a factor of 250.
\[250\div 25=10\]
50 is a factor of 250.
\[250\div 50=5\]
125 is a factor of 250.
\[250\div 125=2\]
250 is a factor of 250.
\[250\div 250=1\]
Thus, the factors of 250 are 1, 2, 5, 10, 25, 50, 125, and 250.
Prime Factorization of 250
The set of prime numbers whose product is 250 is known as the prime factorization of the number 250.
Divide 250 by the smallest prime number possible to get the prime factor of 250. Then, take the result and divide it by the lowest prime number. Repeat this step until we have 1.
The first step is to divide 250 by the lowest prime integer, which is 2.
\[250\div 2=125\]
Divide 125 by 5 because 125 is multiples of 5.
\[125\div 5=25\]
Again divide 25 by 5
\[25\div 5=5\]
Divide 5 by 5
\[5\div 5=1\]
Thus, the prime factorization of 250 is \[2\times 5\times 5\times 5\] or \[2\times {{5}^{3}}\], where 2 and 5 are prime numbers.

Prime Factorization of 250
Prime Factor Tree of 250
Factor trees represent the factors of a number, especially its prime factorization. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops.

Factor Tree of 250
Factors of 250 Pairs
Pair factors may be positive or negative, but they cannot be a fraction or a decimal. To get the pair factor of 250, multiply the two numbers in a pair to obtain the original number, which is 250, as follows:
So, the positive pair factors of 250 are \[\left( 1,\text{ }125 \right),\text{ }\left( 2,\text{ }125 \right),\text{ }\left( 5,\text{ }50 \right)\] and \[\left( 25,\text{ }10 \right)\].
So, the negative pair factors are \[\left( -1,\text{ }-125 \right),\text{ }\left( -2,\text{ }-125 \right),\text{ }\left( -5,\text{ }-50 \right)\] and \[\left( -10,\text{ }-25 \right)\].
Interesting Facts
250 has a total of 8 factors. The total of all 250 factors equals 468.
Remember that 1 is not a prime number and, thus, it will not appear in any factor tree.
Solved Important Questions
1. Find common factors of 150 and 250.
Ans: A factor is an integer that is divided by the original number into equal parts without the remainder. A number that divides each of the provided numbers perfectly is a common factor of two or more numbers.
Hence, factors of 150 and 250 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150, and 1, 2, 5, 10, 25, 50, 125, and 250, respectively.
Therefore, the common factors of 150 and 250 are 1, 2, 5, 10, 25, and 50.
2. What are the factors of 52?
Ans: The factors of 52 are the numbers that divide 52 exactly with no remainder. So,
\[52\div 1=52\]
1 is a factor of 52.
\[52\div 2=26\]
2 is a factor of 52.
4 is a factor of 52.
\[52\div 4=13\]
13 is a factor of 52.
\[52\div 26=2\]
2 is a factor of 52.
\[52\div 52=1\]
52 is a factor of 52.
Therefore, the factors of 52 are 1, 2, 4, 13, 26, and 52.
3. Draw a factor tree of 33.
Solution: Factor trees represent the factors of a number, especially its prime factorization.
Thus, prime factors of 33 are \[3\times 11\].
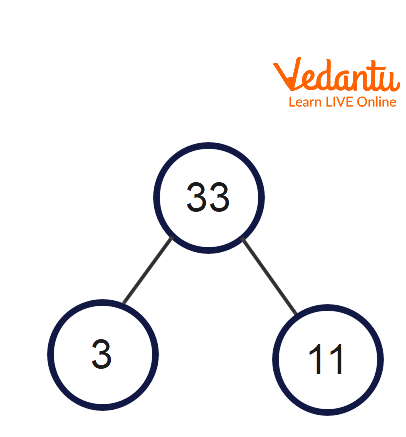
Factor Tree of 33
Conclusion
The numbers that divide 250 exactly with no remainder are known as the factors of 250. The factors of 250 are 1, 2, 5, 10, 25, 50, 125 and 250 and the prime factor of 250 is 2 ✕ 5 ✕ 5 ✕ 5 or 2 ✕ 53, where 2 and 5 are prime numbers. The positive pair factors of 250 are (1, 125), (2, 125), (5, 50) and (25, 10) and the negative pair factors are (-1, -125), (-2, -125), ( -5, -50) and (-25, -10).
Practice Questions
1. How many factors does 250 have?
5
9
8
3
Ans: Option C
2. Is 250 a composite number?
Yes
No
Ans: Option A
FAQs on What Are the Factors of 250?
1. What are the factors of 250?
The factors of 250 are all the whole numbers that divide 250 exactly, leaving no remainder. The complete list of factors for 250 is 1, 2, 5, 10, 25, 50, 125, and 250. Each of these numbers can be multiplied by another whole number to result in 250.
2. How can we find the factors of 250 using the prime factorization method?
The prime factorization method breaks down 250 into a product of its prime factors. The process is as follows:
Start by dividing 250 by the smallest prime number, which is 2: 250 ÷ 2 = 125.
Next, divide the result (125) by the smallest prime factor that can divide it, which is 5: 125 ÷ 5 = 25.
Continue dividing by 5: 25 ÷ 5 = 5.
Finally, divide 5 by itself to reach 1: 5 ÷ 5 = 1.
This gives the prime factorization of 250 as 2 × 5 × 5 × 5, or 2 × 5³. All other factors of 250 can be found by combining these prime factors.
3. How do you create a factor tree for the number 250?
A factor tree is a diagram that visually breaks down a number into its prime factors. To create one for 250:
Write 250 at the top.
Draw two branches down to a pair of factors that multiply to 250, such as 10 and 25.
Since 10 and 25 are not prime numbers, continue branching. Break down 10 into 2 and 5. Both are prime, so these branches end.
Break down 25 into 5 and 5. Both are prime, so these branches also end.
The numbers at the end of the branches (2, 5, 5, 5) are the prime factors of 250.
4. What are the factor pairs of 250?
Factor pairs are the sets of two numbers that multiply together to equal 250. The positive factor pairs of 250 are:
(1, 250)
(2, 125)
(5, 50)
(10, 25)
If negative integers are considered, the pairs would be (-1, -250), (-2, -125), (-5, -50), and (-10, -25).
5. What is the difference between factors and multiples of 250?
The key difference between factors and multiples of 250 lies in the mathematical operation involved:
Factors are numbers that divide 250 without a remainder. They are limited in number and are always less than or equal to 250. For example, 10 is a factor of 250.
Multiples are the result of multiplying 250 by an integer (e.g., 250 × 1, 250 × 2). There are infinitely many multiples, and they are always greater than or equal to 250 (for positive integers). For example, 500 is a multiple of 250.
6. Are the factors of 250 always whole numbers? Can they be negative?
In the context of primary and middle school mathematics (as per the CBSE syllabus), factors are typically defined as positive whole numbers. However, the mathematical definition of factors includes negative integers as well. Since multiplying two negative numbers results in a positive, pairs like (-2) and (-125) are also factors of 250 because (-2) × (-125) = 250. So, while we usually list only the positive factors, every factor has a negative counterpart.
7. How does knowing the prime factors of 250 help in solving other Maths problems, like finding the HCF or LCM?
Knowing the prime factorization of 250 (2 × 5³) is a fundamental skill that helps in solving more complex problems:
Finding HCF (Highest Common Factor): To find the HCF of 250 and another number (e.g., 150 = 2 × 3 × 5²), you multiply the common prime factors raised to their lowest powers. The HCF of 250 and 150 is 2¹ × 5² = 50.
Finding LCM (Lowest Common Multiple): To find the LCM, you multiply all unique prime factors from both numbers raised to their highest powers. The LCM of 250 and 150 is 2¹ × 3¹ × 5³ = 750.
8. Besides the division method and factor tree, are there other ways to check if a number is a factor of 250?
Yes, a quick way to identify some factors of 250 is by using divisibility rules. These rules allow you to check for factors without performing the actual division:
Rule for 2: A number is divisible by 2 if its last digit is even. Since 250 ends in 0, it is divisible by 2.
Rule for 5: A number is divisible by 5 if its last digit is 0 or 5. Since 250 ends in 0, it is divisible by 5.
Rule for 10: A number is divisible by 10 if its last digit is 0. Since 250 ends in 0, it is divisible by 10.
These rules provide a mental shortcut to confirm smaller factors quickly.























