




How to Recognize and Solve Arithmetic Patterns in Numbers
Are you excited to know what an arithmetic pattern means and how to identify different arithmetic patterns? Yes? Okay! Let’s first learn the meaning of a pattern with examples before knowing about arithmetic patterns.
What Are Patterns?
Patterns are repeated arrangements of numbers, objects, lines, colours, shapes, etc. in a logical way.
Look at the picture below to understand patterns in a better way:

Shape pattern
In the above picture, the pattern followed is:
Triangle – Square – Pentagon, Triangle – Square – Pentagon, Triangle – Square – Pentagon.
Here, all shapes like triangle, square, and pentagon are exactly the same.
Arithmetic Pattern or Algebraic Pattern
Do you want to know the other name of the arithmetic pattern?
Yes!
The other name of the arithmetic pattern is “algebraic pattern.”
Now, let’s learn the meaning of arithmetic pattern or algebraic pattern.
Arithmetic Pattern Meaning
Arithmetic pattern or algebraic pattern is a set of numbers that are arranged in order.
For example:
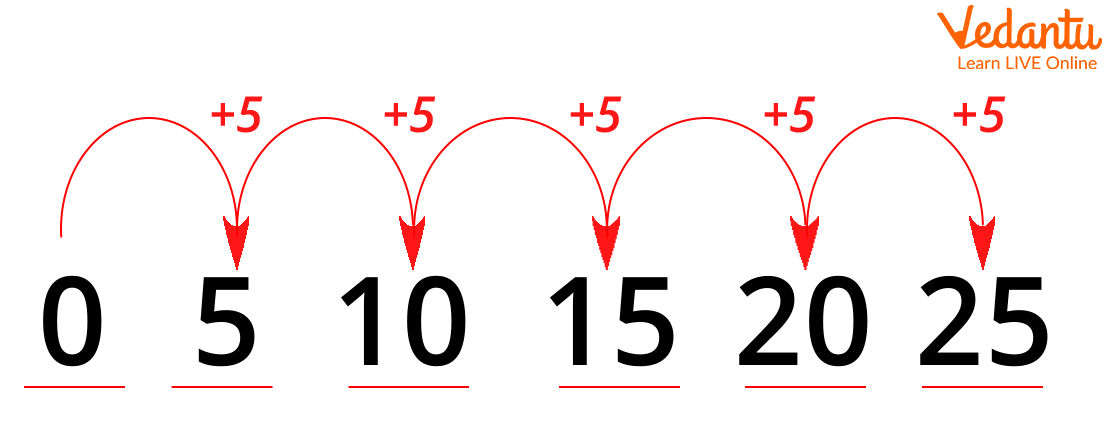
0, 5, 10, 15, 20, 25
The above set of numbers follows some definite pattern.
Are you excited to know “What pattern it follows”? Let’s learn about the pattern.
Here, we used skip counting by 5 to get the next number.
In other words, we get numbers in pattern by adding ‘5’ to get the next number.
Skip counting by 5
Similarly, a different set of numbers follows a different pattern. Let's learn to identify what different patterns a set of numbers can follow with examples.
Arithmetic Patterns with Examples
Let’s learn different arithmetic patterns with examples:
1. Increasing Sequence
In increasing sequence, numbers in a pattern go on increasing. Suppose, you have one football. Now, if your mother gives you two more footballs, it will become three. Again, you received two more footballs from your brother. Now, the total number of footballs you have is 5 ( 1 + 2 + 2). Here, we have observed that the total number of footballs is increasing with each time you are receiving new footballs.
Look at the below picture to understand the increasing sequence pattern in a better way.

Increasing pattern
2. Decreasing Sequence or Decreasing Pattern
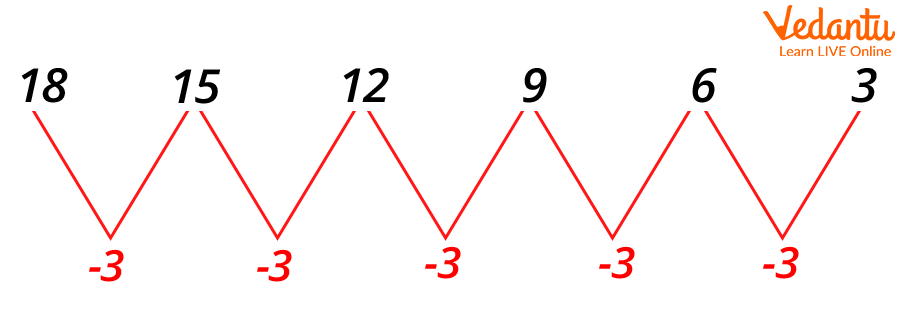
In decreasing sequence, the number in a pattern goes on decreasing. Suppose there are 18 mangoes in the basket. You give three mangoes to each of your friends in the class. The number of mangoes goes on decreasing in the basket each time you give three mangoes to your friend.
Look at the below pattern to understand the decreasing pattern in a better way.
The decreasing pattern is as follows:
Decreasing pattern
In the pattern 18, 15, 12, 9, 6, 3, we have subtracted ‘3’ each time from the previous number to get the next number.
3. Growing Pattern
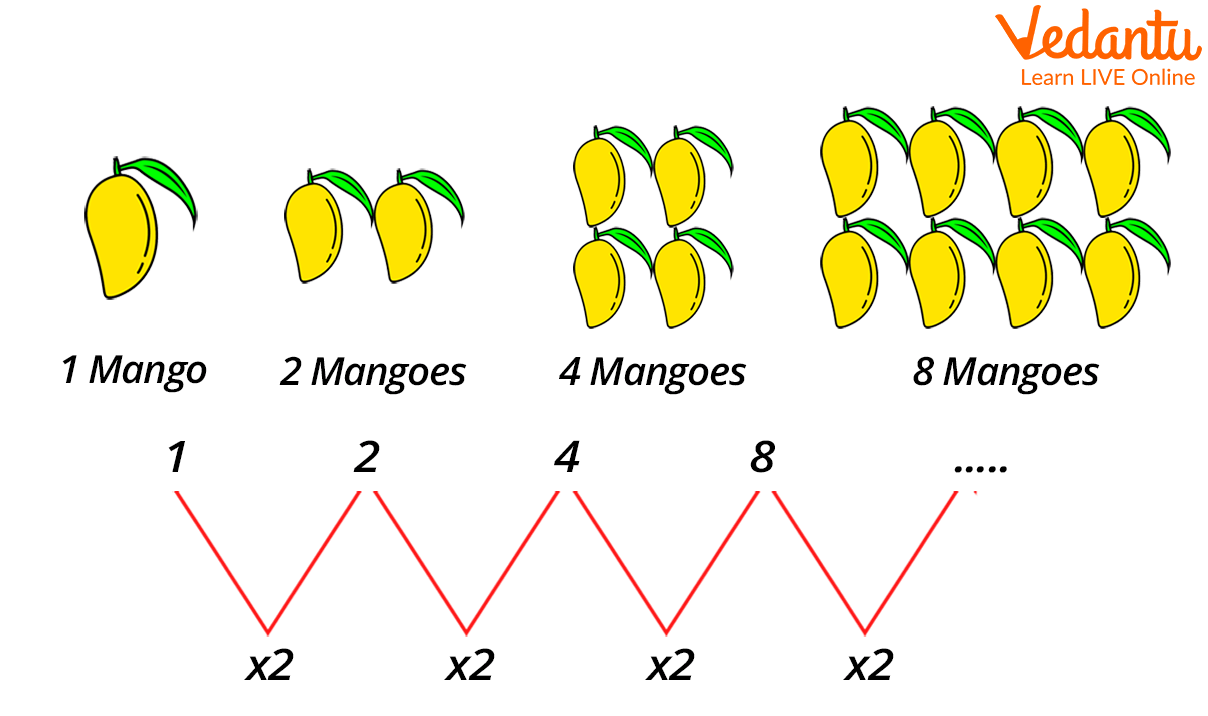
In a growing pattern, the number in a pattern increases rapidly. Here, we multiply the previous number with the same value each time to get the next number.
Look at the below picture to understand the growing pattern in a better way.
Growing pattern
Here,
The pattern 1, 2, 4, 8….. is formed by multiplying two each time.
4. Triangular Pattern
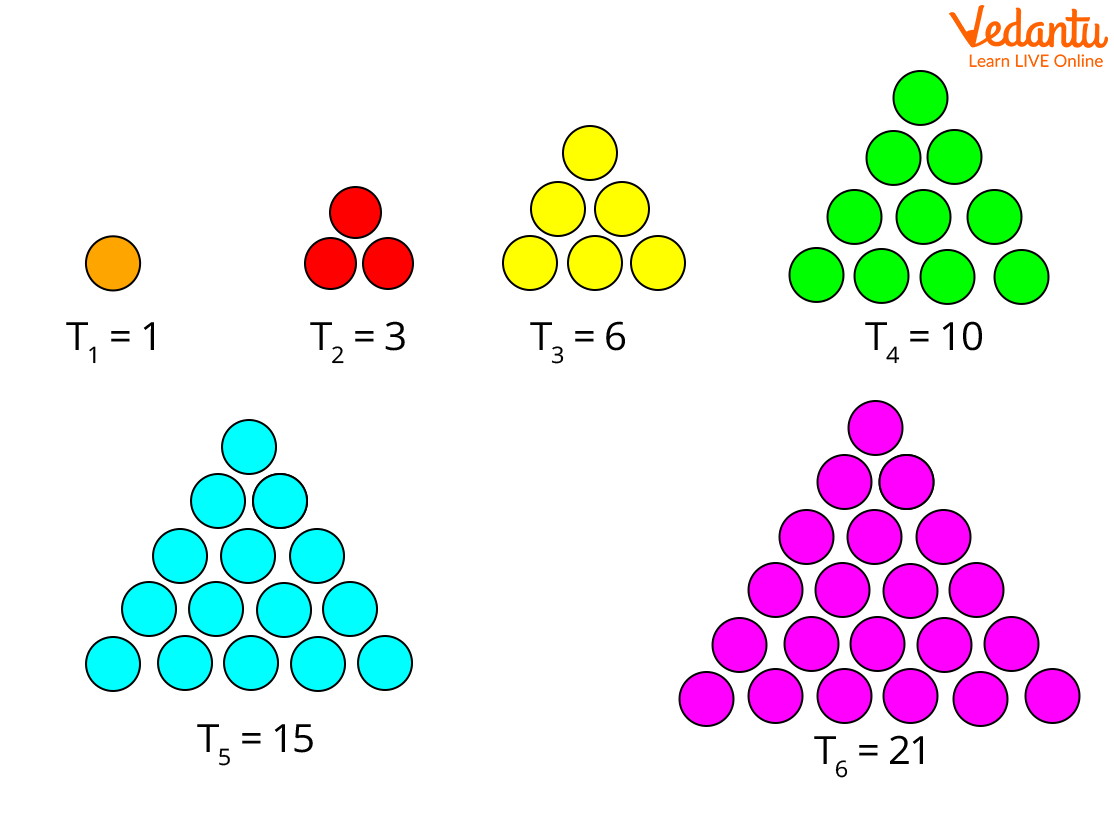
In a triangular pattern, we add another row of dots and count all the dots to find the next number in a given pattern. Let’s understand with an example:
Triangular pattern
Here, the first triangle has only one dot.
In the second triangle, another row is added with 2 extra dots, making 1 + 2 = 3.
In the third triangle, another row is added with 3 extra dots, making 1 + 2 + 3 = 6.
In the fourth triangle, another row is added with 4 extra dots, making 1 + 2 + 3 + 4 = 10.
In the fifth triangle, another row is added with 5 extra dots, making 1 + 2 + 3 + 4 + 5 = 15.
In the sixth triangle, another row is added with 6 extra dots, making 1 + 2 + 3 + 4 + 5 + 6 = 21.
Hence, the pattern here follows: 1, 3, 6, 10, 15, 21….
Conclusion
In short, the arithmetic pattern is the easiest sequence to learn. It creates a string of numbers by adding or subtracting a number from a common difference that relates to one another. For example, the sequence of 3, 5, 7, 9, 12, 14 has a common difference of 2 and the numbers in the sequence are increasing by adding a common difference of 2. If you found this article interesting and wish to read more of such topics, head over to our website and explore from our collection.
FAQs on Master Arithmetic Patterns: Easy Steps & Examples for Students
1. What is an arithmetic pattern in Maths?
An arithmetic pattern, also known as an arithmetic sequence, is a list of numbers where the difference between any two consecutive numbers is always the same. This fixed difference is called the common difference or the 'rule' of the pattern. For example, in the sequence 2, 5, 8, 11, the rule is to add 3 each time.
2. How do you find the rule for a simple arithmetic pattern?
To find the rule of an arithmetic pattern, you need to calculate the difference between consecutive terms. For instance, in the pattern 10, 15, 20, 25:
- Subtract the first term from the second: 15 - 10 = 5.
- Subtract the second term from the third: 20 - 15 = 5.
3. What is the difference between an ascending and a descending arithmetic pattern?
The primary difference is the direction of the number sequence. An ascending pattern is one where the numbers increase, which happens when the rule is to add a positive number (e.g., 4, 8, 12, 16...). A descending pattern is one where the numbers decrease, which happens when the rule is to subtract a number (e.g., 50, 40, 30, 20...).
4. Can you provide some examples of arithmetic patterns in real life?
Yes, arithmetic patterns are very common in daily life. Examples include:
- Saving Money: If you save ₹10 every week, your total savings (₹10, ₹20, ₹30...) form an arithmetic pattern.
- Calendar Dates: The dates for every Sunday in a month (e.g., 7th, 14th, 21st, 28th) follow a pattern with the rule 'add 7'.
- Building Blocks: Stacking layers of blocks where each new layer has two more blocks than the last (2, 4, 6, 8...) creates a visual arithmetic pattern.
5. Why is it so important to identify the 'rule' in a number pattern?
Identifying the rule is the most crucial step because it unlocks the logic of the entire sequence. Once you know the rule, you can not only understand how the pattern is built but also predict any future number in the sequence or find a missing number in the middle. The rule transforms a simple list of numbers into a predictable and logical system.
6. What happens if the difference between numbers keeps changing? Is it still a valid pattern?
Yes, it can still be a valid pattern, but it is not a simple arithmetic pattern. It is likely a growing pattern. For example, in the sequence 1, 2, 4, 7, 11, the amount you add increases each time (+1, +2, +3, +4...). While it has a predictable rule (add the next whole number), it is not an arithmetic pattern because the difference between terms is not constant.
7. Can an arithmetic pattern be made with shapes or objects instead of numbers?
Absolutely. A pattern is any sequence that follows a rule, and this can be represented visually. For example, a sequence showing 1 circle, then 3 circles, then 5 circles is an arithmetic pattern. The underlying mathematical rule is 'add 2', which is applied to the quantity of shapes in each step.























