Question

You have studied in Class $IX$, that a median of a triangle divides it into two triangles of
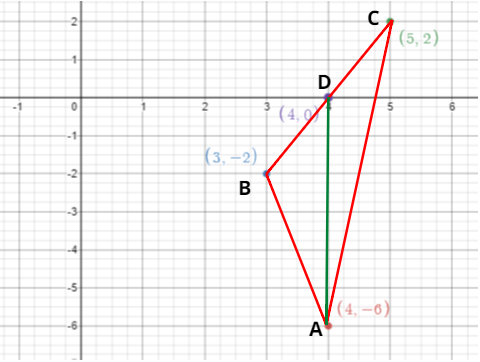
equal areas. Verify this result for $\Delta ABC$ whose vertices are $A(4, - 6),B(3, - 2)$ and $C(5,2)$.

Answer 1

Hint:- Find the midpoint of side BC using midpoint formula.
As we know that for any triangle, the median divides the area of the triangle into two equal parts.
So, we had to prove this for triangle having vertices,
\[ \Rightarrow \]$A(4, - 6),B(3, - 2)$ and $C(5,2)$
So, let AD be the median of this triangle then,
D will be the midpoint of side BC.
Because the median divides the side of the triangle into two equal parts.
So, for finding the value of D,
\[ \Rightarrow D = \left( {\dfrac{{3 + 5}}{2},\dfrac{{ - 2 + 2}}{2}} \right) = (4,0)\]
Now we had to find areas of both the triangles \[\Delta ADB\] and \[\Delta ADC\]. And then compare that,
As we know that for any triangle having three vertices as,
\[ \Rightarrow ({x_1},{y_1}),{\text{ }}({x_2},{y_2})\] and\[{\text{ }}({x_3},{y_3}).\]
\[ \Rightarrow \]Its area will be given as, \[\dfrac{1}{2}\left| {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right|\] (1)
So, for finding the area of the triangle \[\Delta ADB\].
\[ \Rightarrow \]Here, \[({x_1},{y_1}) = (4, - 6);{\text{ }}({x_2},{y_2}) = (4,0);{\text{ }}({x_3},{y_3}) = (3, - 2)\].
So, putting above values in equation 1. We will get,
\[ \Rightarrow \]Area of triangle \[\Delta ADB\]\[ = \dfrac{1}{2}\left| {4(0 + 2) + 4( - 2 + 6) + 3( - 6)} \right|\].
On solving the above equation. We get,
\[ \Rightarrow \]Area of triangle \[\Delta ADB\]\[ = \dfrac{1}{2}\left| 6 \right|\].
\[ \Rightarrow \]Area of triangle \[\Delta ADB\]\[ = 3{\text{ }}unit{s^2}\].
Now, for finding the area of the triangle \[\Delta ADC\].
\[ \Rightarrow \]Here, \[({x_1},{y_1}) = (4, - 6);{\text{ }}({x_2},{y_2}) = (4,0);{\text{ }}({x_3},{y_3}) = (5,2)\].
So, putting above values in equation 1. We get,
\[ \Rightarrow \]Area of triangle \[\Delta ADC\]\[ = \dfrac{1}{2}\left| {4(0 - 2) + 4(2 + 6) + 5( - 6)} \right|\].
On solving the above equation. We get,
\[ \Rightarrow \]Area of triangle \[\Delta ADC\]\[ = \dfrac{1}{2}\left| 6 \right|\].
\[ \Rightarrow \]Area of triangle \[\Delta ADC\]\[ = 3{\text{ }}unit{s^2}\].
Hence, the area of triangle \[\Delta ADC\]= area of triangle \[\Delta ADB\].

Note:- Whenever we came up with this type of problem then the easiest and
efficient way to prove the result is to first find the coordinates of point where
median cuts the given triangle then find the area of both the triangles formed
by the median of the given triangle. Then we can compare both areas to prove our result.