Question

You are asked to “construct” an angle of $90^\circ $. Which of the following methods is considered appropriate for the construction.
1.Using a compass and straightedge, copy an angle that appears to be close to $90^\circ $ from a diagram in your notebook.
2.Using a compass and straightedge, construct two parallel lines and label one of the angles $90^\circ $.
3.Using a compass and straightedge, construct angles of $60^\circ $ and $120^\circ $ and bisect the angle between them.
4.Using a protractor, draw an angle of $90^\circ $.

Answer 1

Hint: Here, in the given question, we need to construct an angle of $90^\circ $ by different methods given in the options. We will construct an angle of $90^\circ $ by one by one by different method and find out which method is appropriate for the construction of an angle of $90^\circ $.

Complete answer:
1.Using a compass and straightedge, copy an angle that appears to be close to $90^\circ $ from a diagram in your notebook.
Let us suppose we are given an angle of $90^\circ $ and we need to copy it using a compass and straightedge.

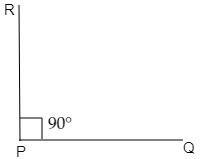
Step 1: Draw a line segment AB of any length.
Step 2: Set the compass point on P and adjust it to any convenient width.
Step 3: Draw an arc across both sides of the angle, creating points J and K.

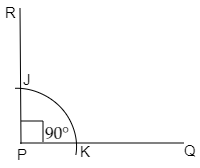
Step 4: Move the compass to A and draw a similar arc, crossing AB at M.
Step 5: Set the compass on K and set its width to J.
Step 6: Move the compass to M and draw an arc crossing the first, creating point L.
Step 7: Draw a ray AC from A through L.

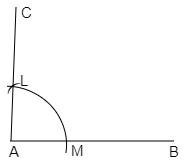
As you can see there is minute difference between both the angles. So from here we can conclude that this method is not appropriate for the construction of an angle.
2.Using a compass and straightedge, construct two parallel lines and label on of the angles $90^\circ $.
As we know angle between two parallel lines is $180^\circ $. Therefore, this method is not appropriate for the construction of an angle of $90^\circ $.
3.Using a compass and straightedge, construct angles of $60^\circ $ and $120^\circ $ and bisect the angle between them.
Step 1: Draw a line segment PQ of any length.
Step 2: Using the compass with any width as radius and with P as a center, draw an arc that cuts the line segment PQ at a point and label it as R.
Step 3: With the same radius and with point R as the center, draw an arc that cuts the previous arc and name it as S.
Step 4: With S as a center and with the same radius draw another arc and name it as T.
Step 5: With the same radius and with S and T as center draw two arcs that cut each other and label it as U.
Step 6: Now join the points U and P. Now we can observe that $\angle UPQ = 90^\circ $.

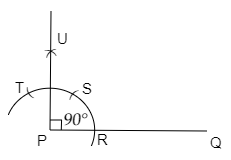
This method is appropriate for the construction of an angle of $90^\circ $.
4.Using a protractor, draw an angle of $90^\circ $.
Step 1: Draw a line segment AB of any measurement.
Step 2: Place the midpoint or center of the protractor on point A.
Step 3: Starting from $0^\circ $ in the protractor, move in the anti-clockwise direction and mark a point in the place of $90^\circ $ as C.
Step 4: Join the points C and A. Now, $\angle CAB$ measures $90^\circ $.

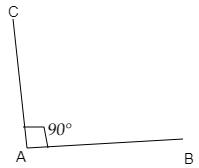
As here you can see we used only protractor to draw an angle of $90^\circ $. As you can see the line segment AB is not straight as it was not drawn using a straightedge. Therefore, this method is not appropriate for construction.

Therefore, the correct option is 3.

Note:
Don’t construct any line segment without using a straightedge. Draw straight lines only by using a straightedge. Don’t use pen instead of pencil, because if any step gets wrong that can be corrected using an eraser. Don’t construct angles by just guessing the angle, use compass.