Question

How do you write $y+2=\dfrac{1}{6}\left( x-4 \right)$ in slope intercept form.

Answer 1

Hint: (1) As in slope intercept form, we represent $y$ in form of $y=mx+c,$
(2) Rewrite the given equation in the form of $y=mx+c,$ by separating the terms.
(3) After rewriting the equation, compare it with general equation of slope intercept form, and then determine the value of $'m'$ and $'c'$

Complete step-by-step solution:
As we have to write,
$y+2=\dfrac{1}{6}\left( x-4 \right)$ in slope intercept form,
As we know that,
Slope intercept form is represented by,
$y=mx+c...(i)$
Where, $y$ and $x$ are variables
$m=$ slope of the graph
$c=y-$intercept
Here,
$y+2=\dfrac{1}{6}\left( x-4 \right)$
$\Rightarrow y+2=\dfrac{1}{6}x-\left( \dfrac{1}{6}\times 4 \right)$
$\Rightarrow y+2=\dfrac{1}{6}x-\dfrac{2}{3}$
$\Rightarrow y=\dfrac{1}{6}x-\dfrac{2}{3}-2$
$\Rightarrow y=\dfrac{1}{6}x-\left[ \dfrac{+2+6}{3} \right]$
$\Rightarrow y=\dfrac{1}{6}x-\dfrac{8}{3}...(ii)$
Now comparing $\left( ii \right)$ with $\left( i \right),$
$y=mx+c$
$y=\dfrac{1}{6}x-\dfrac{8}{3}$
We will get,
$m=$ slope of graph $=\dfrac{1}{6}$
$c=y-$intercept$=\dfrac{-8}{3}$

Therefore the slope intercept form is $y=\dfrac{1}{6}x-\dfrac{8}{3}$.

Note: Slope intercept form is a specific form of linear equation in which we represent in $\left( y=mx+c \right)$ form
$fg.-y=2x+4$
$y=3x-1$
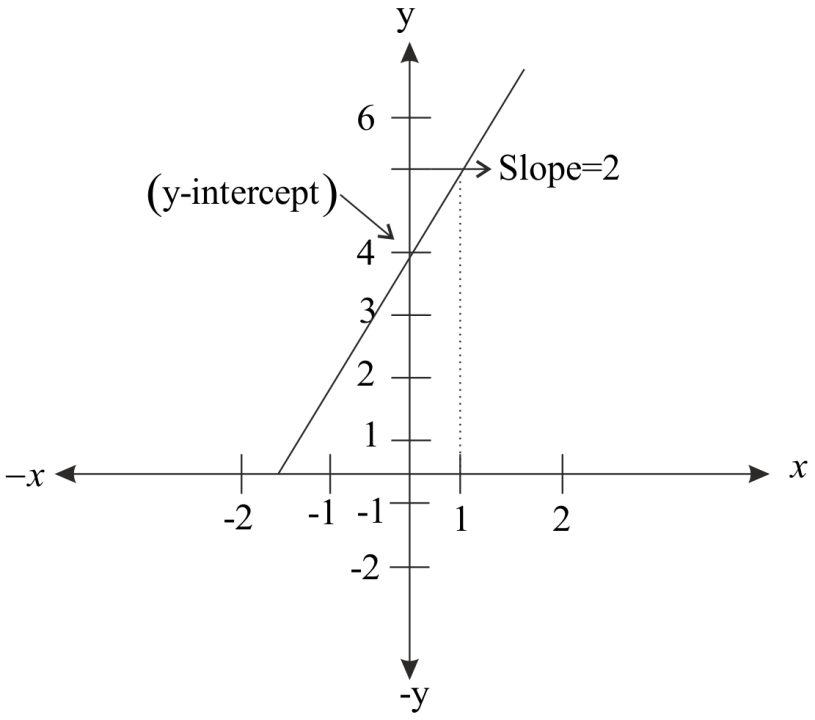
Here, line $y=2x+4,$
Here, slope $2,$ and $y-$intercept $4.$
So, graph will be

Represent only the equation in form of $y=mx+c$ if $y=2x-2,$ Here, $y$ intercepts will be $c=-2$ means, line cuts $y-axis$ at $y=-2$