Question

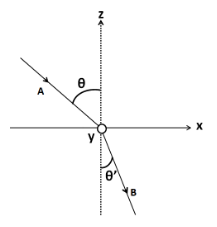
Write the vector representation of the vectors $ A $ and $ B $ with respect to the frame of reference shown in the figure.

(A) $ \vec A = A\sin \theta \hat i - A\cos \theta \hat k $ , $ \vec B = B\sin \theta '\hat j - B\cos \theta '\hat k $
(B) $ \vec A = A\sin \theta \hat i - B\cos \theta \hat k $ , $ \vec B = A\sin \theta '\hat j - B\cos \theta '\hat k $
(C) $ \vec A = B\sin \theta \hat i - A\cos \theta \hat k $ , $ \vec B = B\sin \theta '\hat j - A\cos \theta '\hat k $
(D) $ \vec A = B\sin \theta \hat i - B\cos \theta \hat k $ , $ \vec B = A\sin \theta '\hat j - A\cos \theta '\hat k $

Answer 1

Hint : To solve this question, we need to consider the angles of inclination of the vectors with one axis. Then, multiplying the magnitudes with the cosine and the sine of the angle will respectively give the components along that axis and perpendicular to that axis.

Complete step by step answer
The vector $ A $ is lying in the x-z plane. Therefore, it will have two perpendicular components; one along the direction of the x axis, and the other along the direction of z axis.
Separating the vector $ A $ out of the figure given in the question, we have

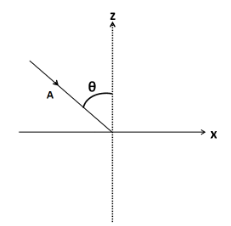
For taking the components, we have to do this vector $ A $ co-initial with the unit vectors, $ \hat i $ and $ \hat k $ . Redrawing the above figure, we get

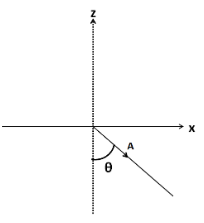
As we can observe, the angle made by vector $ A $ with the x axis is
 $ \varphi = \left( {\dfrac{\pi }{2} - \theta } \right) $
As this angle is in clockwise direction, so we take it to be negative. Therefore
 $ \varphi = - \left( {\dfrac{\pi }{2} - \theta } \right) $ ………………….(1)
Now, the component of $ A $ along the x axis is
 $ {A_x} = A\cos \varphi $
From (1)
 $ {{\rm A}_x} = A\cos \left[ { - \left( {\dfrac{\pi }{2} - \theta } \right)} \right] $
We know that $ \cos \left( { - x} \right) = \cos x $ . Therefore, we get
 $ {{\rm A}_x} = A\cos \left( {\dfrac{\pi }{2} - \theta } \right) $
 $ \Rightarrow {{\rm A}_x} = A\sin \theta $ ………………….(2)
Now, the component along the z axis is
 $ {{\rm A}_z} = A\sin \varphi $
From (1)
 $ {{\rm A}_z} = A\sin \left[ { - \left( {\dfrac{\pi }{2} - \theta } \right)} \right] $
We know that $ \sin \left( { - x} \right) = - \sin x $ . So we get
 $ {{\rm A}_z} = - A\sin \left( {\dfrac{\pi }{2} - \theta } \right) $
 $ \Rightarrow {{\rm A}_z} = - A\cos \theta $ ………………….(3)
Now, the vector $ A $ can be represented as
 $ \vec A = {A_x}\hat i + {A_z}\hat k $
From (2) and (3)
 $ \vec A = A\sin \theta \hat i - A\cos \theta \hat k $
Now, we separate the vector $ B $ out of the given figure

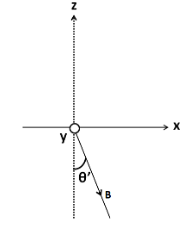
The vector $ B $ is lying in the y-z plane. So it will have two perpendicular components; one along the unit vector $ \hat j $ , and the other along the unit vector $ \hat k $ .
Redrawing the above figure in the y-z plane, we have

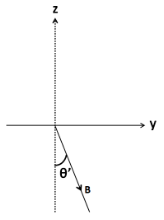
As we can observe, the angle made by vector $ B $ with the y axis is
 $ \varphi ' = \left( {\dfrac{\pi }{2} - \theta '} \right) $
As this angle is in clockwise direction, so we take it to be negative. Therefore
 $ \varphi ' = - \left( {\dfrac{\pi }{2} - \theta '} \right) $ ………………….(4)
Now, the component of $ B $ along the y axis is
 $ {B_y} = B\cos \varphi ' $
From (4)
 $ {B_y} = B\cos \left[ { - \left( {\dfrac{\pi }{2} - \theta '} \right)} \right] $
We know that $ \cos \left( { - x} \right) = \cos x $ . Therefore, we get
 $ {B_y} = B\cos \left( {\dfrac{\pi }{2} - \theta '} \right) $
 $ \Rightarrow {B_y} = B\sin \theta ' $ ………………….(5)
Now, the component along the z axis is
 $ {B_z} = B\sin \varphi ' $
From (4)
 $ {B_z} = B\sin \left[ { - \left( {\dfrac{\pi }{2} - \theta '} \right)} \right] $
We know that $ \sin \left( { - x} \right) = - \sin x $ . So we get
 $ {B_z} = - B\sin \left( {\dfrac{\pi }{2} - \theta '} \right) $
 $ \Rightarrow {B_z} = - B\cos \theta ' $ ………………….(6)
Now, the vector $ A $ can be represented as
 $ \vec B = {B_y}\hat j + {B_z}\hat k $
From (5) and (6)
 $ \vec B = B\sin \theta '\hat j - B\cos \theta '\hat k $ -
Thus, the vector representation of the vectors $ A $ and $ B $ are $ \vec A = A\sin \theta \hat i - A\cos \theta \hat k $ and $ \vec B = B\sin \theta '\hat j - B\cos \theta '\hat k $ .
Hence, the correct answer is option A.

Note
The vector $ B $ appears to be lying in the x-z plane. But the options show that it has one component along the unit vector $ \hat j $ . So from there we got to know that the vector $ B $ is in the y-z plane.