Question

Write the Rutherford -Soddy law of radioactive decay and draw decay curve.

Answer 1

Hint:The Rutherford -Soddy law tells us about the radiation and decay of elements.

Formula used: \[N={{N}_{0}}{{e}^{-\lambda t}}\]

Complete Answer:
1) The radioactivity is based on counting of disintegration per second. The activity depends on the number of decays per second.
2) The law is the exponential decay law which states that a fixed fraction of elements will decay per unit time. Let us take the example, the half part of thorium decays and the remaining in the next four days and so on.

The derivation of the formula: -
\[\begin{align}
  & -\dfrac{dN}{dt}\alpha N \\
 & \Rightarrow -\dfrac{dN}{dt}=kN \\
 & \Rightarrow \int\limits_{{{N}_{0}}}^{N}{\dfrac{dN}{N}}=\lambda \int\limits_{0}^{t}{dt} \\
 & \Rightarrow N={{N}_{0}}{{e}^{-\lambda t}} \\
\end{align}\]
where, N= size of population of radioactive element , N₀= size of initial population of radioactive element, 𝝀 = decay constant.
This shows that the population decays exponentially at a rate that depends on the decay constant.
The time required for half of the population to decay is called the half-life which is given by
\[{{T}_{{}^{1}/{}_{2}}}=\dfrac{0.693}{\lambda }\]
The decay curve is shown in the figure below:

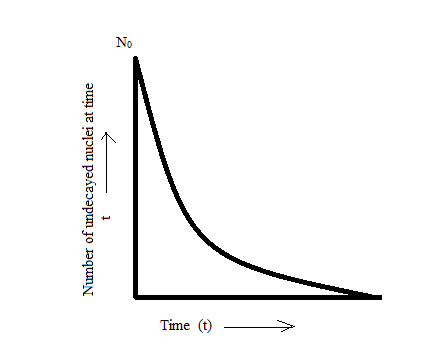
Note: Radioactivity property is exhibited by certain types of matter of emitting energy simultaneously. Half-life is the time required for an element to reduce to half of its initial value.